Rovnicu so stupňom vyšším ako 4 nemožno vo všeobecných radikáloch vyriešiť. Niekedy však stále môžeme nájsť korene polynómu vľavo v rovnici najvyššieho stupňa, ak ho reprezentujeme ako súčin polynómov v stupni maximálne 4. Riešenie týchto rovníc je založené na faktorizácii polynómu na faktory, preto vám odporúčame túto tému zopakovať skôr, ako si prečítate tento článok.

Najčastejšie sa musí človek vysporiadať s rovnicami vyššie stupne s celočíselnými koeficientmi. V týchto prípadoch sa môžeme pokúsiť nájsť racionálne korene a potom faktorovať polynóm, aby sme ho potom transformovali na rovnicu nižšieho stupňa, ktorú bude ľahké vyriešiť. V rámci tohto materiálu budeme zvažovať práve takéto príklady.

Rovnice najvyššieho stupňa s celočíselnými koeficientmi

Všetky rovnice tvaru a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0, môžeme redukovať na rovnicu rovnakého stupňa vynásobením oboch strán a n n - 1 a zmenou premennej tvaru y = a n x:

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 rokov xn + an - 1 rok - 1 xn - 1 +… + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = úzkosť ⇒ yn + bn - 1 rok - 1 +… + b 1 y + b 0 = 0

Výsledné koeficienty budú tiež celé. Budeme teda musieť vyriešiť redukovanú rovnicu n -tého stupňa s celočíselnými koeficientmi, ktorá má tvar x n + a n x n - 1 +… + a 1 x + a 0 = 0.

Vypočítame celé korene rovnice. Ak má rovnica celočíselné korene, musíte ich hľadať medzi deliteľmi voľného výrazu a 0. Zapíšeme si ich a postupne ich nahradíme pôvodnou rovnosťou a skontrolujeme výsledok. Akonáhle získame identitu a nájdeme jeden z koreňov rovnice, môžeme ju napísať v tvare x - x 1 · P n - 1 (x) = 0. Tu x 1 je koreň rovnice a P n - 1 (x) je podiel delenia x n + a n x n - 1 +… + a 1 x + a 0 x - x 1.

Nahraďte zvyšok deliteľov zapísaných v P n - 1 (x) = 0, začínajúc x 1, pretože korene sa môžu opakovať. Po získaní identity sa koreň x 2 považuje za nájdený a rovnicu je možné zapísať v tvare (x - x 1) (x - x 2) P n - 2 (x) = 0. Tu P n - 2 ( x) bude podiel delenia P n - 1 (x) x - x 2.

Pokračujeme v iterácii nad deliteľmi. Nájdite všetky celé korene a označte ich počet ako m. Potom môže byť pôvodná rovnica reprezentovaná ako x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Tu P n - m (x) je polynóm stupňa n - m. Na počítanie je vhodné použiť Hornerovu schému.

Ak má naša pôvodná rovnica celočíselné koeficienty, nemôžeme skončiť so zlomkovými koreňmi.

V dôsledku toho sme dostali rovnicu P n - m (x) = 0, ktorej korene možno nájsť akýmkoľvek vhodným spôsobom. Môžu byť iracionálne alebo zložité.

Ukážme na konkrétnom príklade, ako sa takáto schéma riešenia uplatňuje.

Príklad 1

Stav: nájdite riešenie rovnice x 4 + x 3 + 2 x 2 - x - 3 = 0.

Riešenie

Začnime tým, že nájdeme celé korene.

Máme voľný termín rovný mínus tri. Má delitele 1, - 1, 3 a - 3. Nahraďme ich v pôvodnej rovnici a uvidíme, ktoré z nich vyústia do identít.

S x rovným jednej dostaneme 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, čo znamená, že jeden bude koreňom tejto rovnice.

Teraz vykonáme delenie polynómu x 4 + x 3 + 2 x 2 - x - 3 podľa (x - 1) v stĺpci:

Preto x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4- 1 + 3 = 0

Získali sme identitu, čo znamená, že sme našli ďalší koreň rovnice rovný - 1.

Rozdeľte polynóm x 3 + 2 x 2 + 4 x + 3 o (x + 1) v stĺpci:

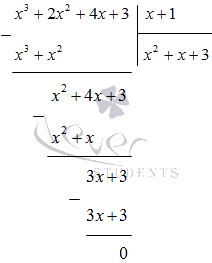
Chápeme to

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Nahraďte ďalšieho deliteľa rovnosťou x 2 + x + 3 = 0, začínajúc - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Výsledné rovnosti budú nesprávne, čo znamená, že rovnica už nemá integrálne korene.

Zostávajúce korene budú koreňmi výrazu x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

Z toho vyplýva, že daný štvorcový trojčlen neexistujú žiadne skutočné korene, ale existujú komplexné konjugované: x = - 1 2 ± i 11 2.

Vysvetlíme, že namiesto dlhého delenia môžeme použiť Hornerovu schému. To sa robí takto: potom, čo sme určili prvý koreň rovnice, vyplníme tabuľku.

V tabuľke koeficientov môžeme hneď vidieť koeficienty podielu delenia polynómov, čo znamená, že x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

Keď nájdeme ďalší koreň rovný - 1, dostaneme nasledujúce:

Odpoveď: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Príklad 2

Stav: Vyriešte rovnicu x 4 - x 3 - 5 x 2 + 12 = 0.

Riešenie

Voľný termín má deliteľov 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

Skontrolujeme ich v poradí:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 ( - 1) 4 - ( - 1) 3 - 5 ( - 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Preto x = 2 bude koreňom rovnice. Rozdelte x 4 - x 3 - 5 x 2 + 12 x - 2 pomocou Hornerovej schémy:

Výsledkom je, že dostaneme x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Preto 2 bude opäť koreň. Rozdelte x 3 + x 2 - 3 x - 6 = 0 x - 2:

Výsledkom je, že dostaneme (x - 2) 2 (x 2 + 3 x + 3) = 0.

Zostávajúce delitele nemá zmysel kontrolovať, pretože rovnosť x 2 + 3 x + 3 = 0 je rýchlejšie a pohodlnejšie riešiť pomocou diskriminátora.

Vyriešime kvadratickú rovnicu:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Získame komplexný konjugovaný pár koreňov: x = - 3 2 ± i 3 2.

Odpoveď: x = - 3 2 ± i 3 2.

Príklad 3

Stav: nájdite skutočné korene pre rovnicu x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Riešenie

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Vykonávame násobenie 2 3 na oboch stranách rovnice:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Nahraďte premenné y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Nakoniec sa nám to podarilo štandardná rovnica 4. stupeň, ktorý je možné vyriešiť podľa štandardnej schémy. Skontrolujme delitele, rozdeľme a získajme nakoniec, že ​​má 2 skutočné korene y = - 2, y = 3 a dva zložité korene. Kompletné riešenie tu nepredstavíme. V dôsledku nahradenia budú skutočné korene tejto rovnice x = y 2 = - 2 2 = - 1 a x = y 2 = 3 2.

Odpoveď: x 1 = - 1, x 2 = 3 2

Ak si v texte všimnete chybu, vyberte ju a stlačte kombináciu klávesov Ctrl + Enter

Zvážte riešenia rovníc s jednou premennou stupňa vyšším ako druhou.

Stupeň rovnice P (x) = 0 je stupeň polynómu P (x), t.j. najväčší zo stupňov jeho výrazov s koeficientom, ktorý sa nerovná nule.

Napríklad rovnica (x 3 - 1) 2 + x 5 = x 6 - 2 má piaty stupeň, pretože po operáciách otvorenia zátvoriek a prinesení podobných dostaneme ekvivalentnú rovnicu x 5 - 2x 3 + 3 = 0 piateho stupňa.

Pripomeňme si pravidlá, ktoré budú potrebné na riešenie rovníc vyšších ako dvoch.

Vyhlásenia o koreňoch polynómu a jeho deliteľoch:

1. N -tý polynóm stupeň má počet koreňov najviac n a korene multiplicity m sa vyskytujú presne m krát.

2. Polynom nepárneho stupňa má najmenej jeden skutočný koreň.

3. Ak α je koreň P (x), potom P n (x) = (x - α) Q n - 1 (x), kde Q n - 1 (x) je polynóm stupňa (n - 1).

4.

5. Redukovaný polynóm s celočíselnými koeficientmi nemôže mať zlomkové racionálne korene.

6. Pre polynóm stupňa 3

P 3 (x) = sekera 3 + bx 2 + cx + d je možná jedna z dvoch vecí: buď sa rozloží na súčin troch binomických čísel

Р 3 (x) = а (х - α) (х - β) (х - γ), alebo sa dá rozložiť na súčin binomického a štvorcového trinomického Р3 (x) = а (х - α) (х 2 + βх + γ).

7. Akýkoľvek polynóm štvrtého stupňa je možné rozložiť na súčin dvoch štvorcových trojčlenov.

8. Polynóm f (x) je deliteľný polynomom g (x) bezo zvyšku, ak existuje polynóm q (x) taký, že f (x) = g (x) q (x). Na delenie polynómov sa používa pravidlo „rohové delenie“.

9. Na deliteľnosť polynómu P (x) na binomický (x - c) je potrebné a dostatočné, aby číslo c bolo koreňom P (x) (dôsledok Bezoutovej vety).

10. Vietova veta: Ak x 1, x 2, ..., x n sú skutočné korene polynómu

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, potom platia nasledujúce rovnosti:

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0.

Príklady riešenia

Príklad 1.

Nájdite zvyšok delenia P (x) = x 3 + 2/3 x 2 - 1/9 podľa (x - 1/3).

Riešenie.

Na základe Bezoutovej vety: „Zvyšok delenia polynómu binomickým číslom (x - c) sa rovná hodnote polynómu v c“. Nájdeme Р (1/3) = 0. Preto je zvyšok 0 a číslo 1/3 je koreň polynomu.

Odpoveď: R = 0.

Príklad 2.

Rozdeľte rohom 2x 3 + 3x 2 - 2x + 3 podľa (x + 2). Nájdite zvyšok a neúplný kvocient.

Riešenie:

2x 3 + 3x 2 - 2x + 3 | x + 2

2 x 3 + 4 x 2 2x 2 - x

X 2 - 2 x

Odpoveď: R = 3; súkromné: 2x 2 - x.

Základné metódy riešenia rovníc vyšších stupňov

1. Predstavujeme novú premennú

Spôsob zavedenia novej premennej je už známy na príklade biquadratických rovníc. Spočíva v tom, že na vyriešenie rovnice f (x) = 0 sa zavedie nová premenná (substitúcia) t = xn alebo t = g (x) a f (x) sa vyjadrí t, získa sa nová rovnica r (t). Potom po vyriešení rovnice r (t) nájdeme korene:

(t 1, t 2, ..., t n). Potom sa získa množina n rovníc q (x) = t 1, q (x) = t 2, ..., q (x) = t n, z ktorých sa nachádzajú korene pôvodnej rovnice.

Príklad 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Riešenie:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Náhrada (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 = 2, t 2 = 1. Spätná výmena:

x 2 + x + 1 = 2 alebo x 2 + x + 1 = 1;

x 2 + x - 1 = 0 alebo x 2 + x = 0;

Odpoveď: Z prvej rovnice: x 1, 2 = (-1 ± √5) / 2, z druhej: 0 a -1.

2. Faktorizácia zoskupením a redukované multiplikačné vzorce

Základ táto metóda nie je tiež nový a spočíva v zoskupení výrazov takým spôsobom, že každá skupina obsahuje spoločný faktor. Aby ste to urobili, niekedy musíte použiť niektoré umelé metódy.

Príklad 1.

x 4 - 3x 2 + 4x - 3 = 0.

Riešenie.

Predstavte si - 3x 2 = -2x 2 - x 2 a skupinu:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 = 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 = 0 alebo x 2 + x - 3 = 0.

Odpoveď: V prvej rovnici nie sú žiadne korene, z druhej: x 1, 2 = (-1 ± √13) / 2.

3. Faktoring metódou nedefinovaných koeficientov

Podstata metódy spočíva v tom, že pôvodný polynóm sa rozloží na faktory s neznámymi koeficientmi. Na základe vlastnosti, že polynomy sú rovnaké, ak sú ich koeficienty rovnaké v rovnakých stupňoch, sa nájdu neznáme koeficienty expanzie.

Príklad 1.

x 3 + 4x 2 + 5x + 2 = 0.

Riešenie.

Polynom 3. stupňa je možné rozšíriť na súčin lineárneho a štvorcového faktora.

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - sekera 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

Po vyriešení systému:

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, t.j.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

Korene rovnice (x + 1) (x 2 + 3x + 2) = 0 sa dajú ľahko nájsť.

Odpoveď: -1; -2.

4. Spôsob výberu koreňa najvyšším a voľným koeficientom

Metóda je založená na aplikácii viet:

1) Akýkoľvek celočíselný koreň polynómu s celočíselnými koeficientmi je deliteľom voľného výrazu.

2) Aby bola neredukovateľná frakcia p / q (p je celé číslo, q je prirodzené číslo) koreňom rovnice s celočíselnými koeficientmi, je potrebné, aby číslo p bolo celočíselným deliteľom voľného výrazu a 0, a q - prirodzený deliteľ vedúceho koeficientu.

Príklad 1.

6x 3 + 7x 2 - 9x + 2 = 0.

Riešenie:

6: q = 1, 2, 3, 6.

Preto p/q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6.

Keď sme našli jeden koreň, napríklad - 2, nájdeme ďalšie korene pomocou delenia podľa uhla, metódy nedefinovaných koeficientov alebo Hornerovej schémy.

Odpoveď: -2; 1/2; 1/3.

Stále máte otázky? Nie ste si istí, ako riešiť rovnice?
Ak chcete získať pomoc od tútora - zaregistrujte sa.
Prvá lekcia je zadarmo!

stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.

Na kanáli YouTube nášho webu, aby ste mali prehľad o všetkých nových lekciách videa.

Na začiatok si pripomeňme základné vzorce stupňov a ich vlastnosti.

Produkt čísla a stane sa to n krát, môžeme tento výraz napísať ako a a ... a = a n

1.a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7. a n / a m = a n - m

Výkon alebo exponenciálne rovnice - sú to rovnice, v ktorých sú premenné v mocninách (alebo exponentoch) a základom je číslo.

Príklady exponenciálnych rovníc:

V. tento príkladčíslo 6 je základňa, vždy stojí v spodnej časti a premenná X stupeň alebo indikátor.

Tu je niekoľko ďalších príkladov exponenciálnych rovníc.
2 x * 5 = 10
16 x - 4 x - 6 = 0

Teraz sa pozrime na to, ako sú vyriešené exponenciálne rovnice?

Zoberme si jednoduchú rovnicu:

2 x = 2 3

Takýto príklad je možné vyriešiť aj v mysli. Je vidieť, že x = 3. Koniec koncov, aby bola ľavá a pravá strana rovnaká, musíte namiesto x dať číslo 3.
Teraz sa pozrime, ako je potrebné toto riešenie formalizovať:

2 x = 2 3
x = 3

Aby sme takúto rovnicu vyriešili, odstránili sme identické dôvody(teda dvojky) a zapísali si, čo zostalo, to sú stupne. Dostali sme požadovanú odpoveď.

Teraz si zhrňme naše rozhodnutie.

Algoritmus na riešenie exponenciálnej rovnice:
1. Potreba skontrolovať rovnakýči má rovnica základy vpravo a vľavo. Ak dôvody nie sú rovnaké, hľadáme možnosti, ako tento príklad vyriešiť.
2. Potom, čo sú základy rovnaké, rovnať stupeň a vyriešte výslednú novú rovnicu.

Teraz vyriešime niekoľko príkladov:

Začnime jednoducho.

Základne na ľavej a pravej strane sa rovnajú číslu 2, čo znamená, že môžeme odhodiť základňu a porovnať ich stupne.

x + 2 = 4 Toto je najjednoduchšia rovnica.
x = 4 - 2
x = 2
Odpoveď: x = 2

V nasledujúcom príklade vidíte, že základy sú rôzne, sú 3 a 9.

3 3x - 9x + 8 = 0

Najprv prenesieme deväť na pravú stranu a získame:

Teraz musíte urobiť rovnaké základy. Vieme, že 9 = 3 2. Použime vzorec stupňov (a n) m = a nm.

3 x = (3 2) x + 8

Dostaneme 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 teraz vidíte, že základne na ľavej a pravej strane sú rovnaké a rovnajú sa trom, takže ich môžeme zahodiť a dať stupňom rovnakú váhu.

3x = 2x + 16 má najjednoduchšiu rovnicu
3x - 2x = 16
x = 16
Odpoveď: x = 16.

Pozrite sa na nasledujúci príklad:

2 2x + 4 - 10 4 x = 2 4

Najprv sa pozrieme na základne, základne sú dve a štyri. A my musíme byť - rovnakí. Štvorku prepočítajte podľa vzorca (a n) m = a nm.

4 x = (2 2) x = 2 2x

A tiež používame jeden vzorec a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Pridajte k rovnici:

2 2x 2 4 - 10 2 2x = 24

Uviedli sme príklad na rovnaké dôvody. Prekážajú nám však ostatné čísla 10 a 24. Čo s nimi? Ak sa pozriete pozorne, vidíte, že na ľavej strane opakujeme 2 x, tu je odpoveď - 2 x, ktoré môžeme vybrať zo zátvoriek:

2 2x (2 4 - 10) = 24

Vypočítajme výraz v zátvorkách:

2 4 — 10 = 16 — 10 = 6

Rozdelte celú rovnicu na 6:

Predstavme si 4 = 2 2:

2 2x = 2 2 bázy sú rovnaké, zahodíme ich a porovnáme mocniny.
2x = 2 dostaneme najjednoduchšiu rovnicu. Rozdelíme to na 2, čo dostaneme
x = 1
Odpoveď: x = 1.

Vyriešme rovnicu:

9 x - 12 * 3 x + 27 = 0

Transformujme:
9 x = (3 2) x = 3 2x

Dostaneme rovnicu:
3 2x - 12 3x +27 = 0

Naše základy sú rovnaké ako 3. V tomto prípade môžete vidieť, že prvé tri majú stupeň dvakrát (2x) ako druhé (len x). V takom prípade môžete vyriešiť náhradná metóda... Nahraďte číslo najmenším stupňom:

Potom 3 2x = (3x) 2 = t 2

Nahraďte všetky mocniny x v rovnici s t:

t 2 - 12t + 27 = 0
Dostaneme kvadratickú rovnicu. Riešime pomocou diskriminátora a dostaneme:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Návrat k premennej X.

Berieme t 1:
t 1 = 9 = 3 x

To znamená,

3 x = 9
3 x = 3 2
x 1 = 2

Našiel sa jeden koreň. Hľadáme druhé, z t 2:
t2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Odpoveď: x 1 = 2; x 2 = 1.

Na webe môžete v sekcii POMOC RIEŠIŤ klásť otázky, ktoré vás zaujímajú, vám určite odpovieme.

Pripojte sa ku skupine

Súdiac podľa začiatku publikácie, ktorú tu vynechávame, text napísal Yuri Ignatievich. A je to napísané dobre a problém je aktuálny, len tak sa dá nazvať Rusko, ako to robí Mukhin ...

Bez ohľadu na to, ako sa niekto správa k protiľudovej moci, Rusko je nad ňou a nezaslúži si urážky. Aj od talentovaného whistleblowera americkej agentúry NASA.

*

Adresa súdruhovi Mukhin Yu.I.

Vážený Jurij Ignatievič! Viem, že navštevujete tieto stránky. Preto sa obraciam priamo na vás.

Všetci oceňujeme vašu obetavú prácu v oblasti odhaľovania klamstiev Západu, klamstiev Ameriky, klamstiev pseudovedcov a klamstiev liberálov. S potešením a prospechom pre seba a spoločnosť myslíme na vážne témy, ktoré na nás z času na čas vrhnete, či už ide o zásluhovosť alebo metafyziku, lásku k národná história alebo obnovenie spravodlivosti.

Vaše definície našej spoločnej vlasti sú však mätúce a veľmi znepokojujúce.

Však posúďte sami: ako by ste charakterizovali človeka, ktorý začal urážať svoju matku, ktorá bola chorá a kvôli tomu dočasne prestala pracovať?

Ale Rusko, bez ohľadu na to, ako sa to nazýva, a bez ohľadu na to, aká dobrá alebo nechutná je vláda, Rusko je našou vlasťou. Vlasť. Naši starí otcovia pre ňu preliali krv a položili život.

Zrovnanie s mocou má teda znamenať zníženie duchovného vznešenia na úroveň materiálneho, ba dokonca nízku. Títo. porovnávaš úplne iné kategórie. Vec, ktorá je pre každého rozumného človeka neprijateľná.

Pýtam sa vás, drahý súdruh. Mukhin, vážne o tom premýšľaj.

**

... A s rovnicami (toto som nevedel) je situácia nasledovná. Ako nájsť korene kvadratická rovnica hádal už v starovekom Egypte.

Ako nájsť korene kubickej rovnice a rovnice štvrtého stupňa bolo nájdené v šestnástom storočí, ale korene rovnice piateho stupňa našli až v roku 2016. A ďaleko od bežných ľudí sa snažil.

V šestnástom storočí sa zakladateľ symbolickej algebry François Viet pokúsil nájsť korene rovnice piateho stupňa; v devätnástom storočí sa zakladateľ modernej vyššej algebry, francúzsky matematik Evariste Galois, pokúsil nájsť korene rovnice piateho stupňa; po ňom sa nórsky matematik Niels Henrik Abel pokúsil vzdať a dokázal nemožnosť riešenia rovnice piateho stupňa v r. všeobecný pohľad.

Na Wikipédii čítame o zásluhách Ábela: „Abel dokončil brilantnú štúdiu starodávneho problému:dokázal nemožnosť riešiť vo všeobecnej forme (v radikáloch) rovnicu 5. stupňa ...

V algebre Abel našiel potrebnú podmienku, aby bol koreň rovnice vyjadrený „v radikáloch“ pomocou koeficientov tejto rovnice. Dostatočnú podmienku čoskoro objavil Galois, ktorého úspechy boli založené na dielach Ábela.

Abel uviedol konkrétne príklady rovnice 5. stupňa, ktorej korene nemožno vyjadriť v radikáloch, a tým do značnej miery uzatvoril starodávny problém. “

Ako vidíte, ak sa pokúšali neustále dokazovať Poincaréovu vetu a ukázalo sa, že Perelman má viac šťastia ako ostatní matematici, potom po Ábelovi neberú do úvahy rovnice piateho stupňa matematiky.

A v roku 2014 matematik z Tomska Sergej Zaikov, o ktorom z fotky môžete usúdiť, že už má roky, a podľa údajov z článku o ňom, že je absolventom fakulty aplikovaná matematika a kybernetika Tomska štátna univerzita, v priebehu svojej práce získal rovnice piateho stupňa. Slepá ulica? Áno, slepá ulička! Sergej Zaikov sa však zaviazal, že to zlomí.

A v roku 2016 našiel spôsoby, ako riešiť rovnice piateho stupňa vo všeobecnej forme! Urobil to, čo matematici Galois a Ábel dokázali ako nemožné.

Pokúšal som sa nájsť informácie o Sergejovi Zaikovovi na Wikipédii, ale šukám vás! O matematikovi Sergejovi Zaikovovi a o jeho nájdení riešenia rovníc piateho stupňa žiadna informácia!

Skutočnosť, že pre matematikov existuje analóg nobelová cena -Abelova cena(Nobel zakázal udeľovať cenu matematikom a teraz sa udeľuje za matematické výkaly, nazýva sa ich „fyzika“).

Táto matematická cena je na počesť samotného Ábela, ktorý dokázal nemožnosť toho, čo Zaikov urobil... Samostatná nominácia na túto cenu však nie je povolená. A Zaikov je osamelý matematik a neexistujú žiadne organizácie, ktoré by ho mohli navrhnúť ako kandidáta na túto cenu.

Pravda, máme Akadémiu vied, ale koniec koncov, akademici tam nesedia kvôli rozvoju matematiky, ale „aby uťali korisť“. Kto tam potrebuje tohto Zaikova?

No, pre tlačové agentúry Zaikov nie je Perelman pre vás! Zaikovov objav pre médiá preto nie je senzáciou.

Že Porošenko urobil chybu vo dverách - áno! Toto je skutočná senzácia!

Tomský matematik vyriešil problém, ktorý nebolo možné vyriešiť dvesto rokov

S nástupom algebry sa za jej hlavnú úlohu považovalo riešenie algebraických rovníc. Riešenie rovnice druhého stupňa bolo známe už v Babylone a Staroveký Egypt... V škole prechádzame takýmito rovnicami. Pamätáte si rovnicu x2 + ax + b = 0 a diskriminačný prvok?

Sergej Zaikov s knihou

Riešenie algebraických rovníc tretieho a štvrtého stupňa bolo nájdené v šestnástom storočí. Rovnicu piateho stupňa však nebolo možné vyriešiť. Dôvod zistil Lagrange. Ukázal, že riešenie rovníc tretieho a štvrtého stupňa bolo možné, pretože ich je možné redukovať na rovnice, ktoré už boli vyriešené. Rovnicu tretieho stupňa je možné redukovať na rovnicu druhého stupňa a rovnicu štvrtého stupňa na rovnicu tretieho. Rovnica piateho stupňa sa však redukuje na rovnicu šiesteho, to znamená zložitejšej, preto tradičné metódy riešenia nie sú použiteľné.

Otázka riešenia rovnice piateho stupňa sa pohla dopredu iba pred dvesto rokmi, keď Abel dokázal, že nie všetky rovnice piateho stupňa je možné vyriešiť v radikáloch, to znamená v štvorcových, kubických a iných koreňoch, ktoré sú nám známe z škola. A Galois čoskoro, to znamená pred dvesto rokmi, našiel kritérium na určenie, ktoré rovnice piateho stupňa je možné v radikáloch vyriešiť a ktoré nie. Spočíva v tom, že Galoisova skupina, rozpustná v radikáloch rovnice piateho stupňa, musí byť buď cyklická alebo metacyklická. Galois ale nenašiel spôsob, ako v radikáloch vyriešiť tie rovnice piateho stupňa, ktoré sú v radikáloch riešiteľné. Galoisova teória je veľmi slávna, bolo o nej napísaných veľa kníh.

Doteraz boli pre rovnice piateho stupňa riešiteľné v radikáloch nájdené iba konkrétne riešenia. A iba v tomto roku tomský matematik Sergej Zaikov vyriešil problém, ktorý nebolo možné vyriešiť dvesto rokov. Vydala knihu „Ako sa riešia v radikáloch? algebraické rovnice piateho stupňa “, v ktorom naznačil metódu riešenia pre akékoľvek rovnice piateho stupňa, ktoré sú rozpustné v radikáloch. Zaikov je absolventom Fakulty aplikovanej matematiky a kybernetiky na Štátnej univerzite Tomsk. Podarilo sa nám s ním urobiť rozhovor.

- Sergey, prečo ste začali riešiť tento problém?

- Potreboval som vyriešiť rovnicu piateho stupňa na vyriešenie úlohy z iného odvetvia matematiky. Začal som zisťovať, ako to nájsť, a zistil som, že nie všetci sú vyriešení v radikáloch. Potom som skúsil hľadať vedecká literatúra metóda na riešenie rovníc, ktoré sú rozpustné v radikáloch, ale našli iba kritérium, pomocou ktorého je možné určiť, ktoré sú rozpustné a ktoré nie. Nie som algebraista, ale samozrejme, ako absolvent FPMK môžem uplatňovať aj algebraické metódy. Preto som od roku 2014 začal vážne hľadať riešenie a našiel som ho sám.

Metódu som našiel pred dvoma rokmi, pripravil som knihu, v ktorej bola nielen popísaná, ale aj spôsoby riešenia niektorých rovníc stupňov väčších ako piata. Ale nemal som peniaze na to, aby som to zverejnil. Tento rok som sa rozhodol, že bude jednoduchšie publikovať iba časť tejto práce, a zobral som z nej iba polovicu, venovanú metóde riešenia rovnice piateho stupňa v radikáloch.

Dal som si za cieľ vydať niečo ako návod na riešenie tohto problému, zrozumiteľný pre matematikov, ktorí potrebujú vyriešiť konkrétnu rovnicu. Preto som to zjednodušil odstránením mnohých dlhé vzorce a veľa z teórie, obmedzenie viac ako polovice a ponechanie len toho najnutnejšieho. Preto som skončil s niečím ako s knihou „pre atrapy“, podľa ktorej matematici, ktorí nie sú oboznámení s Galoisovou teóriou, dokážu vyriešiť potrebnú rovnicu.

- Za to patrí veľká vďaka Vladislavovi Beresnevovi, s ktorým sa poznáme mnoho rokov. Sponzoroval vydanie knihy.

- Je možné, aby ste za vyriešenie tohto problému získali akúkoľvek cenu za matematiku? Spomenuli ste napríklad Ábela. Existuje však Abelova cena za matematiku, ktorá sa považuje za analóg Nobelovej ceny?

- Túto možnosť nemožno úplne vylúčiť. Ale nemali by ste v to ani dúfať.

Napríklad prihlášky na kandidátov na Ábelovu cenu 2019 je potrebné podať do 15. septembra. Okrem toho nie je povolená vlastná nominácia. A som osamelý matematik. Neexistujú žiadne organizácie ani známi matematici, ktorí by ma nominovali. Preto sa nebude zvažovať bez ohľadu na to, či si moja práca toto ocenenie zaslúži, a či je v duchu tohto ocenenia udeliť ho tým, ktorí pokračujú v Ábelovej práci. Ale aj keď je prezentovaný, všetko závisí aj od úrovne práce ostatných kandidátov.

Kniha je určená pre tých, ktorí nie sú oboznámení s Galoisovou teóriou. Základy Galoisovej teórie sú uvedené iba v časti, v ktorej sú potrebné na riešenie rovnice, podrobne je popísaná metóda riešenia a sú ukázané techniky, ktoré riešenie zjednodušujú. Veľká časť knihy je venovaná príkladu riešenia konkrétnej rovnice. Recenzentmi knihy sú doktor technických vied Gennadij Petrovič Agibalov a doktor fyziky. mat. Vedy, profesor Petr Andreevič Krylov.

PRIPRAVENÉ ANASTASIA SKIRNEVSKAYA