In general, an equation with a degree higher than 4 cannot be solved in radicals. But sometimes we can still find the roots of the polynomial on the left in the equation of the highest degree, if we represent it as a product of polynomials in degree at most 4. The solution to such equations is based on factoring a polynomial into factors, so we advise you to repeat this topic before studying this article.

Most often, one has to deal with the equations higher degrees with integer coefficients. In these cases, we can try to find the rational roots, and then factor the polynomial in order to then transform it into an equation of a lower degree, which will be easy to solve. Within the framework of this material, we will consider just such examples.

Equations of the highest degree with integer coefficients

All equations of the form a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0, we can reduce to an equation of the same degree by multiplying both sides by a n n - 1 and changing a variable of the form y = a n x:

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 +… + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 +… + b 1 y + b 0 = 0

The resulting coefficients will also be whole. Thus, we will need to solve the reduced equation of the nth degree with integer coefficients, which has the form x n + a n x n - 1 +… + a 1 x + a 0 = 0.

We calculate the whole roots of the equation. If the equation has integer roots, you need to look for them among the divisors of the free term a 0. Let us write them down and substitute them into the original equality in turn, checking the result. Once we have obtained an identity and found one of the roots of the equation, we can write it in the form x - x 1 · P n - 1 (x) = 0. Here x 1 is the root of the equation, and P n - 1 (x) is the quotient of dividing x n + a n x n - 1 +… + a 1 x + a 0 by x - x 1.

Substitute the rest of the divisors written out in P n - 1 (x) = 0, starting with x 1, since the roots can be repeated. After obtaining the identity, the root x 2 is considered found, and the equation can be written as (x - x 1) (x - x 2) P n - 2 (x) = 0. Here P n - 2 (x) will be the quotient of dividing P n - 1 (x) by x - x 2.

We continue to iterate over the divisors. Find all whole roots and denote their number as m. After that, the original equation can be represented as x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Here P n - m (x) is a polynomial of degree n - m. It is convenient to use Horner's scheme for counting.

If our original equation has integer coefficients, we cannot end up with fractional roots.

As a result, we got the equation P n - m (x) = 0, the roots of which can be found in any convenient way. They can be irrational or complex.

Let us show with a specific example how such a solution scheme is applied.

Example 1

Condition: find the solution to the equation x 4 + x 3 + 2 x 2 - x - 3 = 0.

Solution

Let's start by finding whole roots.

We have a free term equal to minus three. It has divisors of 1, - 1, 3, and - 3. Let's substitute them in the original equation and see which of them will result in identities.

With x equal to one, we get 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, which means that one will be the root of this equation.

Now we perform division of the polynomial x 4 + x 3 + 2 x 2 - x - 3 by (x - 1) in a column:

Hence, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

We have obtained an identity, which means that we have found another root of the equation, equal to - 1.

Divide the polynomial x 3 + 2 x 2 + 4 x + 3 by (x + 1) in a column:

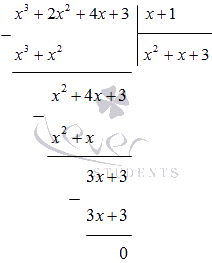
We get that

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Substitute the next divisor into the equality x 2 + x + 3 = 0, starting with - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

The resulting equalities will be incorrect, which means that the equation no longer has integral roots.

The remaining roots will be the roots of the expression x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

It follows from this that the given square trinomial there are no real roots, but there are complex conjugate ones: x = - 1 2 ± i 11 2.

Let us clarify that instead of long division, Horner's scheme can be used. This is done like this: after we have determined the first root of the equation, we fill in the table.

In the table of coefficients, we can immediately see the coefficients of the quotient of the division of polynomials, which means that x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

After finding the next root equal to - 1, we get the following:

Answer: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Example 2

Condition: Solve the equation x 4 - x 3 - 5 x 2 + 12 = 0.

Solution

The free term has divisors 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

We check them in order:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Hence, x = 2 will be the root of the equation. Divide x 4 - x 3 - 5 x 2 + 12 by x - 2 using Horner's scheme:

As a result, we get x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Hence, 2 will again be a root. Divide x 3 + x 2 - 3 x - 6 = 0 by x - 2:

As a result, we get (x - 2) 2 (x 2 + 3 x + 3) = 0.

It makes no sense to check the remaining divisors, since the equality x 2 + 3 x + 3 = 0 is faster and more convenient to solve using the discriminant.

Let's solve the quadratic equation:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

We get a complex conjugate pair of roots: x = - 3 2 ± i 3 2.

Answer: x = - 3 2 ± i 3 2.

Example 3

Condition: find the real roots for the equation x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Solution

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

We carry out multiplication 2 3 of both sides of the equation:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Replace the variables y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

In the end, we succeeded standard equation 4th degree, which can be solved according to the standard scheme. Let's check the divisors, divide and get in the end that it has 2 real roots y = - 2, y = 3 and two complex roots. We will not present the complete solution here. Due to the replacement, the real roots of this equation will be x = y 2 = - 2 2 = - 1 and x = y 2 = 3 2.

Answer: x 1 = - 1, x 2 = 3 2

If you notice an error in the text, please select it and press Ctrl + Enter

Consider solutions of equations with one variable of degree higher than the second.

The degree of the equation P (x) = 0 is the degree of the polynomial P (x), i.e. the largest of the degrees of its terms with a coefficient not equal to zero.

So, for example, the equation (x 3 - 1) 2 + x 5 = x 6 - 2 has the fifth degree, because after the operations of opening the brackets and bringing similar ones, we get the equivalent equation x 5 - 2x 3 + 3 = 0 of the fifth degree.

Let us recall the rules that will be needed to solve equations of degree higher than two.

Statements about the roots of a polynomial and its divisors:

1. Nth polynomial degree has the number of roots at most n, and the roots of multiplicity m occur exactly m times.

2. An odd degree polynomial has at least one real root.

3. If α is a root of P (x), then P n (x) = (x - α) Q n - 1 (x), where Q n - 1 (x) is a polynomial of degree (n - 1).

4.

5. The reduced polynomial with integer coefficients cannot have fractional rational roots.

6. For a polynomial of degree 3

P 3 (x) = ax 3 + bx 2 + cx + d one of two things is possible: either it decomposes into a product of three binomials

Р 3 (x) = а (х - α) (х - β) (х - γ), or it can be decomposed into the product of a binomial and a square trinomial Р 3 (x) = а (х - α) (х 2 + βх + γ ).

7. Any polynomial of the fourth degree can be decomposed into the product of two square trinomials.

8. The polynomial f (x) is divisible by the polynomial g (x) without a remainder if there is a polynomial q (x) such that f (x) = g (x) q (x). For dividing polynomials, the “corner division” rule is applied.

9. For the divisibility of the polynomial P (x) into the binomial (x - c), it is necessary and sufficient that the number c be a root of P (x) (Corollary of Bezout's theorem).

10. Vieta's theorem: If x 1, x 2, ..., x n are real roots of the polynomial

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, then the following equalities hold:

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0.

Solution examples

Example 1.

Find the remainder of dividing P (x) = x 3 + 2/3 x 2 - 1/9 by (x - 1/3).

Solution.

By corollary to Bezout's theorem: "The remainder of dividing a polynomial by a binomial (x - c) is equal to the value of the polynomial in c". Let's find Р (1/3) = 0. Therefore, the remainder is 0 and the number 1/3 is the root of the polynomial.

Answer: R = 0.

Example 2.

Divide with a corner 2x 3 + 3x 2 - 2x + 3 by (x + 2). Find the remainder and the incomplete quotient.

Solution:

2x 3 + 3x 2 - 2x + 3 | x + 2

2х 3 + 4 x 2 2x 2 - x

X 2 - 2 x

Answer: R = 3; private: 2x 2 - x.

Basic methods for solving equations of higher degrees

1. Introducing a new variable

The method of introducing a new variable is already familiar with the example of biquadratic equations. It consists in the fact that to solve the equation f (x) = 0, a new variable (substitution) t = x n or t = g (x) is introduced and f (x) is expressed in terms of t, obtaining a new equation r (t). Then, solving the equation r (t), the roots are found:

(t 1, t 2, ..., t n). After that, a set of n equations q (x) = t 1, q (x) = t 2, ..., q (x) = t n is obtained, from which the roots of the original equation are found.

Example 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Solution:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Replacement (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 = 2, t 2 = 1. Reverse replacement:

x 2 + x + 1 = 2 or x 2 + x + 1 = 1;

x 2 + x - 1 = 0 or x 2 + x = 0;

Answer: From the first equation: x 1, 2 = (-1 ± √5) / 2, from the second: 0 and -1.

2. Factorization by grouping and reduced multiplication formulas

The foundation this method is also not new and consists in grouping the terms in such a way that each group contains a common factor. To do this, sometimes you have to use some artificial methods.

Example 1.

x 4 - 3x 2 + 4x - 3 = 0.

Solution.

Imagine - 3x 2 = -2x 2 - x 2 and group:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 = 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 = 0 or x 2 + x - 3 = 0.

Answer: There are no roots in the first equation, from the second: x 1, 2 = (-1 ± √13) / 2.

3. Factoring by the method of undefined coefficients

The essence of the method is that the original polynomial is decomposed into factors with unknown coefficients. Using the property that the polynomials are equal if their coefficients are equal at the same degrees, the unknown expansion coefficients are found.

Example 1.

x 3 + 4x 2 + 5x + 2 = 0.

Solution.

A polynomial of the 3rd degree can be decomposed into the product of a linear and a square factor.

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

Having solved the system:

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, i.e.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

The roots of the equation (x + 1) (x 2 + 3x + 2) = 0 are easy to find.

Answer: -1; -2.

4. Method of selection of the root by the highest and the free coefficient

The method is based on the application of theorems:

1) Any integer root of a polynomial with integer coefficients is a divisor of the free term.

2) In order for the irreducible fraction p / q (p is an integer, q is a natural) to be a root of an equation with integer coefficients, it is necessary that the number p be an integer divisor of the free term a 0, and q is a natural divisor of the leading coefficient.

Example 1.

6x 3 + 7x 2 - 9x + 2 = 0.

Solution:

6: q = 1, 2, 3, 6.

Therefore, p / q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6.

Having found one root, for example - 2, we find other roots using division with an angle, the method of undefined coefficients or Horner's scheme.

Answer: -2; 1/2; 1/3.

Still have questions? Not sure how to solve equations?
To get help from a tutor - register.
The first lesson is free!

site, with full or partial copying of the material, a link to the source is required.

On the youtube channel of our site, to keep abreast of all the new video lessons.

To begin with, let's recall the basic formulas of degrees and their properties.

Product of a number a happens to itself n times, we can write this expression as a a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Power or exponential equations - these are equations in which the variables are in powers (or exponents), and the base is a number.

Examples of exponential equations:

V this example the number 6 is the base, it always stands at the bottom, and the variable x degree or indicator.

Here are some more examples of exponential equations.
2 x * 5 = 10
16 x - 4 x - 6 = 0

Now let's look at how the exponential equations are solved?

Let's take a simple equation:

2 x = 2 3

Such an example can be solved even in the mind. It can be seen that x = 3. After all, in order for the left and right sides to be equal, you need to put the number 3 instead of x.
Now let's see how this solution needs to be formalized:

2 x = 2 3
x = 3

In order to solve such an equation, we removed identical grounds(that is, deuces) and wrote down what was left, these are degrees. We got the desired answer.

Now let's summarize our decision.

Algorithm for solving the exponential equation:
1. Need to check the same whether the equation has bases on the right and left. If the grounds are not the same, we are looking for options to solve this example.
2. After the bases are the same, equate degree and solve the resulting new equation.

Now let's solve a few examples:

Let's start simple.

The bases on the left and right sides are equal to the number 2, which means we can discard the base and equate their degrees.

x + 2 = 4 This is the simplest equation.
x = 4 - 2
x = 2
Answer: x = 2

In the following example, you can see that the bases are different, they are 3 and 9.

3 3x - 9x + 8 = 0

To begin with, we transfer the nine to the right side, we get:

Now you need to make the same bases. We know that 9 = 3 2. Let's use the formula of degrees (a n) m = a nm.

3 3x = (3 2) x + 8

We get 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 now you can see that the bases on the left and right sides are the same and equal to three, so we can discard them and equate the degrees.

3x = 2x + 16 got the simplest equation
3x - 2x = 16
x = 16
Answer: x = 16.

See the following example:

2 2x + 4 - 10 4 x = 2 4

First of all, we look at the bases, bases are different two and four. And we need to be - the same. Convert the four by the formula (a n) m = a nm.

4 x = (2 2) x = 2 2x

And we also use one formula a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Add to the equation:

2 2x 2 4 - 10 2 2x = 24

We have brought the example to the same grounds. But we are hindered by other numbers 10 and 24. What to do with them? If you look closely, you can see that on the left side we repeat 2 2x, here is the answer - 2 2x we can take out of the brackets:

2 2x (2 4 - 10) = 24

Let's calculate the expression in brackets:

2 4 — 10 = 16 — 10 = 6

Divide the whole equation by 6:

Let's imagine 4 = 2 2:

2 2x = 2 2 bases are the same, we discard them and equate the powers.
2x = 2 we get the simplest equation. We divide it by 2 we get
x = 1
Answer: x = 1.

Let's solve the equation:

9 x - 12 * 3 x + 27 = 0

Let's transform:
9 x = (3 2) x = 3 2x

We get the equation:
3 2x - 12 3x +27 = 0

Our bases are the same equal to 3. In this example, you can see that the first three has a degree twice (2x) than the second (just x). In this case, you can solve replacement method... Replace the number with the smallest degree:

Then 3 2x = (3x) 2 = t 2

Replace all powers with x in the equation with t:

t 2 - 12t + 27 = 0
We get a quadratic equation. We solve through the discriminant, we get:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Returning to the variable x.

We take t 1:
t 1 = 9 = 3 x

That is,

3 x = 9
3 x = 3 2
x 1 = 2

Found one root. We are looking for the second, from t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Answer: x 1 = 2; x 2 = 1.

On the site you can in the section HELP TO SOLVE to ask questions of interest, we will definitely answer you.

Join the group

Judging by the beginning of the publication, which we omit here, the text was written by Yuri Ignatievich. And it is written well, and the problematic is topical, that's the only way to call Russia, as Mukhin does ...

No matter how anyone treats the anti-people power, Russia is above it and does not deserve insults. Even from the talented whistleblower of the American agency NASA.

*

Address to Comrade Mukhin Yu.I.

Dear Yuri Ignatievich! I know that you are visiting these pages. Therefore, I am addressing you directly.

We all appreciate your selfless work in the field of exposing the lies of the West, the lies of America, the lies of pseudoscientists, and the lies of liberals. With pleasure and benefit for ourselves and society, we think about serious topics that you throw at us from time to time, be it meritocracy or metaphysics, love for national history or restoration of justice.

However, your definitions of our common homeland are perplexing and very upsetting.

However, judge for yourself: how would you characterize a person who began to insult his mother, who was sick and temporarily stopped working because of this?

But Russia, no matter how it is called, and no matter how good or disgusting the government is, Russia is our Motherland. Motherland. For her, our grandfathers shed blood and laid their lives.

Therefore, putting it on a par with power is to lower the spiritual sublime to the level of the material, and even low. Those. you are comparing completely different categories. A thing that is unacceptable for any sane person.

I ask you, dear comrade. Mukhin, seriously think about this.

**

... And with equations (I did not know this) the situation is as follows. How to find roots quadratic equation guessed back in ancient Egypt.

How to find the roots of the cubic equation and the equation of the fourth degree was found in the sixteenth century, but they could not find the roots of the equation of the fifth degree until 2016. And far from ordinary people tried.

In the sixteenth century, the founder of symbolic algebra, François Viet, tried to find the roots of the fifth-degree equation; in the nineteenth century, the founder of modern higher algebra, the French mathematician Evariste Galois, tried to find the roots of the fifth-degree equations; after him, the Norwegian mathematician Niels Henrik Abel tried gave up and proved the impossibility of solving an equation of the fifth degree in general view.

We read in Wikipedia about the merits of Abel: “Abel completed a brilliant study of an ancient problem:proved the impossibility to solve in general form (in radicals) the equation of the 5th degree ...

In algebra, Abel found a necessary condition for the root of an equation to be expressed "in radicals" in terms of the coefficients of this equation. The sufficient condition was soon discovered by Galois, whose achievements were based on the works of Abel.

Abel gave specific examples of a 5th-degree equation, whose roots cannot be expressed in radicals, and thus largely closed the ancient problem. "

As you can see, if they tried to prove Poincaré's theorem all the time and Perelman turned out to be luckier than the rest of the mathematicians, then after Abel the mathematicians did not take up the equations of the fifth degree.

And in 2014 mathematician from Tomsk Sergey Zaikov, about whom you can judge from the photo that he is already in years, and according to the data from the article about him, that he is a graduate of the faculty applied mathematics and cybernetics of Tomsk state university, in the course of his work he obtained equations of the fifth degree. Dead end? Yes, dead end! But Sergei Zaikov undertook to break it.

And in 2016 he found ways to solve equations of the fifth degree in general form! He did what the mathematicians Galois and Abel proved impossible.

I tried to find information about Sergei Zaikov on Wikipedia, but fuck you! On the mathematician Sergei Zaikov and on his finding a solution to equations of the fifth degree no information!

The fact that for mathematicians there is an analogue of Nobel Prize -Abel Prize(Nobel forbade giving the prize to mathematicians and now it is given for mathematical feces, calling them "physics").

This mathematical prize is in honor of the very Abel who proved the impossibility of what Zaikov did... However, self-nomination for this award is not allowed. And Zaikov is a lone mathematician and there are no organizations that could propose him as a candidate for this prize.

True, we have the Academy of Sciences, but the academics do not sit there for the development of mathematics, but "to saw the loot." Who needs this Zaikov there?

Well, for news agencies Zaikov is not Perelman for you! Therefore, Zaikov's discovery for the media is not a sensation.

That Poroshenko made a mistake with the door - yes! This is a real sensation!

Tomsk mathematician solved a problem that could not be solved for two hundred years

With the advent of algebra, its main task was considered to be the solution of algebraic equations. The solution to an equation of the second degree was already known in Babylon and Ancient egypt... We go through such equations in school. Remember the equation x2 + ax + b = 0, and the discriminant?

Sergei Zaikov with a book

The solution to algebraic equations of the third and fourth degrees was found in the sixteenth century. But it was not possible to solve the equation of the fifth degree. The reason was found by Lagrange. He showed that the solution of equations of the third and fourth degrees became possible because they can be reduced to equations that have already been solved. An equation of the third degree can be reduced to an equation of the second degree, and an equation of the fourth to an equation of the third. But the equation of the fifth degree is reduced to the equation of the sixth, that is, more complex, so the traditional methods of solution are not applicable.

The question of solving an equation of the fifth degree got under way only two hundred years ago, when Abel proved that not all equations of the fifth degree can be solved in radicals, that is, in square, cubic and other roots, known to us from school. And Galois soon, that is, two hundred years ago, found a criterion for determining which equations of the fifth degree can be solved in radicals and which cannot. It consists in the fact that the Galois group, solvable in radicals of an equation of the fifth degree, must be either cyclic or metacyclic. But Galois did not find a way to solve in radicals those equations of the fifth degree that are solvable in radicals. Galois theory is very famous, many books have been written about it.

Until now, only particular solutions have been found for equations of the fifth degree solvable in radicals. And only this year, the Tomsk mathematician Sergei Zaikov solved a problem that could not be solved for two hundred years. Published the book “How are they solved in radicals? algebraic equations of the fifth degree ”, in which he indicated a method for solving for any equations of the fifth degree, which are solvable in radicals. Zaikov is a graduate of the Faculty of Applied Mathematics and Cybernetics, Tomsk State University. We managed to interview him.

- Sergey, why did you start solving this problem?

- I needed to solve a fifth-degree equation to solve a problem from another branch of mathematics. I started figuring out how to find it and found out that not all of them are solved in radicals. Then I tried to search in scientific literature a method for solving those equations that are solvable in radicals, but found only a criterion by which one can determine which are solvable and which are not. I am not an algebraist, but, of course, as a graduate of the FPMK, I can also apply algebraic methods. Therefore, since 2014, I started looking for a solution in earnest and found it myself.

The method was found by me two years ago, I prepared a book in which not only it was described, but also ways of solving some equations of degrees greater than the fifth. But I had no money to publish it. This year I decided that it would be easier to publish only a part of this work, and took only half of it, devoted to the way to solve the equation of the fifth degree in radicals.

I set out to publish something like a guide to solving this problem, understandable for mathematicians who need to solve a specific equation. Therefore, I simplified it by removing many long formulas and much of the theory, cutting back more than half, leaving only the essentials. Therefore, I ended up with something like a book "for dummies", according to which mathematicians who are not familiar with Galois theory can solve the equation they need.

- For this, many thanks to Vladislav Beresnev, with whom we have known for many years. He sponsored the publication of the book.

- Is it possible for you to receive any prize in mathematics for solving this problem? For example, you mentioned Abel. But is there an Abel Prize in mathematics, which is considered an analogue of the Nobel Prize?

- This possibility cannot be completely ruled out. But you shouldn't hope for it either.

For example, applications for candidates for the 2019 Abel Prize must be submitted by September 15th. Moreover, self-nomination is not allowed. And I'm a lone mathematician. There are no organizations or well-known mathematicians who will nominate me. Therefore, it will not be considered regardless of whether my work deserves this award, and whether it is in the spirit of this award to award it to those who continue Abel's work. But even if it is presented, everything also depends on the level of work of other candidates.

The book is intended for those who are not familiar with Galois theory. The fundamentals of Galois theory are given only in the part in which they are necessary for solving the equation, the solution method is described in detail, and techniques are shown that simplify the solution. Much of the book is devoted to the example of solving a specific equation. The book's reviewers are Doctor of Technical Sciences Gennady Petrovich Agibalov and Doctor of Phys. mat. Sciences, Professor Petr Andreevich Krylov.

PREPARED ANASTASIA SKIRNEVSKAYA