По принцип уравнение със степен по-висока от 4 не може да бъде решено в радикали. Но понякога все още можем да намерим корените на полинома вляво в уравнението на най -високата степен, ако го представим като произведение на полиноми в степен най -много 4. Решението на такива уравнения се основава на разлагането на полином във фактори, така че ви съветваме да повторите тази тема, преди да изучавате тази статия.

Най-често човек трябва да се справя с уравненията по-високи степенис цели коефициенти. В тези случаи можем да се опитаме да намерим рационалните корени и след това да разложим полинома на множители, за да го трансформираме в уравнение от по-ниска степен, което ще бъде лесно за решаване. В рамките на този материал ще разгледаме точно такива примери.

Уравнения от най-висока степен с цели коефициенти

Всички уравнения от вида a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0, можем да намалим до уравнение със същата степен, като умножим двете страни по a n n - 1 и променим променлива от формата y = a n x:

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 +… + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 +… + b 1 y + b 0 = 0

Получените коефициенти също ще бъдат цели. По този начин ще трябва да решим редуцираното уравнение от n-та степен с цели коефициенти, което има вида x n + a n x n - 1 +… + a 1 x + a 0 = 0.

Изчисляваме всички корени на уравнението. Ако уравнението има цели числа, трябва да ги потърсите сред делителите на свободния член a 0. Нека ги запишем и ги заместим в оригиналното равенство на свой ред, като проверим резултата. След като получим идентичност и намерим един от корените на уравнението, можем да го запишем във формата x - x 1 · P n - 1 (x) = 0. Тук x 1 е коренът на уравнението, а P n - 1 (x) е частното от деленето на x n + a n x n - 1 +… + a 1 x + a 0 на x - x 1.

Заместете останалите делители, записани в P n - 1 (x) = 0, започвайки с x 1, тъй като корените могат да се повторят. След получаване на идентичността, коренът x 2 се счита за намерен и уравнението може да се запише във вида (x - x 1) (x - x 2) P n - 2 (x) = 0. Тук P n - 2 ( x) ще бъде частното от разделянето на P n - 1 (x) на x - x 2.

Продължаваме да повтаряме делителите. Намерете всички цели корени и означете техния брой като m. След това оригиналното уравнение може да бъде представено като x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Тук P n - m (x) е полином от степен n - m. За броене е удобно да се използва схемата на Хорнер.

Ако нашето първоначално уравнение има целочислени коефициенти, не можем да завършим с дробни корени.

В резултат на това получихме уравнението P n - m (x) = 0, чиито корени могат да бъдат намерени по всеки удобен начин. Те могат да бъдат ирационални или сложни.

Нека покажем с конкретен пример как се прилага такава схема на решение.

Пример 1

състояние:намерете решението на уравнението x 4 + x 3 + 2 x 2 - x - 3 = 0.

Решение

Нека започнем с намирането на цели корени.

Имаме свободен член, равен на минус три. Има делители на 1, - 1, 3 и - 3. Нека ги заместим в оригиналното уравнение и да видим кое от тях ще доведе до идентичности.

При x равно на единица получаваме 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, което означава, че един ще бъде коренът на това уравнение.

Сега извършваме деление на полинома x 4 + x 3 + 2 x 2 - x - 3 на (x - 1) в колона:

Следователно, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4- 1 + 3 = 0

Получихме тождество, което означава, че сме намерили друг корен на уравнението, равен на - 1.

Разделете полинома x 3 + 2 x 2 + 4 x + 3 на (x + 1) в колона:

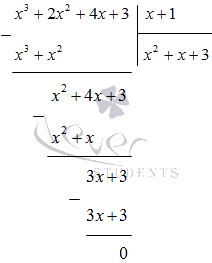
Ние разбираме това

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Заменете следващия делител в равенството x 2 + x + 3 = 0, започвайки с - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Получените равенства ще бъдат неправилни, което означава, че уравнението вече няма интегрални корени.

Останалите корени ще бъдат корените на израза x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

От това следва, че даденото квадратен триномняма реални корени, но има сложни спрегнати: x = - 1 2 ± i 11 2.

Нека уточним, че вместо дълго деление може да се използва схемата на Хорнер. Това става така: след като сме определили първия корен на уравнението, попълваме таблицата.

В таблицата с коефициентите веднага можем да видим коефициентите на частното от деление на полиноми, което означава, че x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

След като намерим следващия корен, равен на - 1, получаваме следното:

Отговор: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Пример 2

състояние:Решете уравнението x 4 - x 3 - 5 x 2 + 12 = 0.

Решение

Свободният член има делители 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

Проверяваме ги по ред:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Следователно, x = 2 ще бъде коренът на уравнението. Разделете x 4 - x 3 - 5 x 2 + 12 на x - 2, като използвате схемата на Хорнер:

В резултат получаваме x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Следователно 2 отново ще бъде корен. Разделете x 3 + x 2 - 3 x - 6 = 0 на x - 2:

В резултат получаваме (x - 2) 2 (x 2 + 3 x + 3) = 0.

Няма смисъл да проверявате останалите делители, тъй като равенството x 2 + 3 x + 3 = 0 е по -бързо и по -удобно за решаване с помощта на дискриминанта.

Нека решим квадратното уравнение:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Получаваме комплексно спрегната двойка корени: x = - 3 2 ± i 3 2.

Отговор: x = - 3 2 ± i 3 2.

Пример 3

състояние:намерете реалните корени на уравнението x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Решение

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Извършваме умножение 2 3 от двете страни на уравнението:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Заменете променливите y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

В крайна сметка успяхме стандартно уравнение 4-та степен, която може да се реши по стандартната схема. Нека проверим делителите, разделим и накрая получим, че има 2 реални корена y = - 2, y = 3 и два комплексни корена. Тук няма да представяме цялостното решение. Поради замяната, реалните корени на това уравнение ще бъдат x = y 2 = - 2 2 = - 1 и x = y 2 = 3 2.

Отговор: x 1 = - 1, x 2 = 3 2

Ако забележите грешка в текста, моля, изберете я и натиснете Ctrl + Enter

Обмисли решения на уравнения с една променлива степен по -висока от втората.

Степента на уравнението P (x) = 0 е степента на полинома P (x), т.е. най -голямата от степени на нейните членове с коефициент, който не е равен на нула.

Така, например, уравнението (x 3 - 1) 2 + x 5 = x 6 - 2 има пета степен, т.к. след операциите за отваряне на скоби и довеждане на подобни, получаваме еквивалентното уравнение x 5 - 2x 3 + 3 = 0 от пета степен.

Нека си припомним правилата, които ще са необходими за решаване на уравнения от степен по-висока от две.

Твърдения за корените на полином и неговите делители:

1. N-ти полиномстепен има броя на корените най-много n, а корените от кратност m се срещат точно m пъти.

2. Полином с нечетна степен има поне един реален корен.

3. Ако α е корен от P (x), тогава P n (x) = (x - α) Q n - 1 (x), където Q n - 1 (x) е полином от степен (n - 1).

4.

5. Редуцираният полином с цели коефициенти не може да има дробни рационални корени.

6. За полином от степен 3

P 3 (x) = ax 3 + bx 2 + cx + d е възможно едно от двете неща: или се разлага на продукт от три бинома

Р 3 (x) = а (х - α) (х - β) (х - γ), или може да се разложи на произведение на бином и квадратен тричлен Р 3 (x) = а (х - α) (х 2 + βх + γ ).

7. Всеки полином от четвърта степен може да бъде разложен на произведение на два квадратни тринома.

8. Полиномът f (x) се дели на полинома g (x) без остатък, ако има полином q (x) такъв, че f (x) = g (x) q (x). За разделянето на полиноми се прилага правилото „деление на ъгъла“.

9. За делимостта на полинома P (x) на бином (x - c), е необходимо и достатъчно числото c да бъде корен от P (x) (Следствие от теоремата на Безут).

10. Теоремата на Виета: Ако x 1, x 2, ..., x n са реални корени на полинома

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, тогава са валидни следните равенства:

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0.

Примери за решения

Пример 1.

Намерете остатъка от разделянето на P (x) = x 3 + 2/3 x 2 - 1/9 на (x - 1/3).

Решение.

Като следствие от теоремата на Безут: „Остатъкът от разделянето на полином на бином (x - c) е равен на стойността на полинома в c“. Да намерим Р (1/3) = 0. Следователно остатъкът е 0 и числото 1/3 е коренът на полинома.

Отговор: R = 0.

Пример 2.

Разделете с ъгъл 2x 3 + 3x 2 - 2x + 3 с (x + 2). Намерете остатъка и непълното частно.

Решение:

2x 3 + 3x 2 - 2x + 3 | х + 2

2x 3 + 4 x 2 2x 2 - x

Х 2 - 2 х

Отговор: R = 3; частни: 2x 2 - x.

Основни методи за решаване на уравнения от по-високи степени

1. Въвеждане на нова променлива

Методът за въвеждане на нова променлива вече е запознат с примера на биквадратни уравнения. Състои се във факта, че за решаване на уравнението f (x) = 0 се въвежда нова променлива (заместване) t = xn или t = g (x) и f (x) се изразява чрез t, като се получава нова уравнение r (t). След това, решавайки уравнението r (t), се намират корените:

(t 1, t 2, ..., t n). След това се получава набор от n уравнения q (x) = t 1, q (x) = t 2, ..., q (x) = t n, от които се намират корените на оригиналното уравнение.

Пример 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Решение:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Замяна (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 = 2, t 2 = 1. Обратна замяна:

x 2 + x + 1 = 2 или x 2 + x + 1 = 1;

x 2 + x - 1 = 0 или x 2 + x = 0;

Отговор: От първото уравнение: x 1, 2 = (-1 ± √5) / 2, от второто: 0 и -1.

2. Разлагане на множители чрез групиране и формули за намалено умножение

Фондацията този методсъщо не е ново и се състои в групиране на термините по такъв начин, че всяка група да съдържа общ фактор. За да направите това, понякога трябва да използвате някои изкуствени методи.

Пример 1.

x 4 - 3x 2 + 4x - 3 = 0.

Решение.

Представете си - 3x 2 = -2x 2 - x 2 и групирайте:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 = 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 = 0 или x 2 + x - 3 = 0.

Отговор: В първото уравнение няма корени, от второто: x 1, 2 = (-1 ± √13) / 2.

3. Факторизиране по метода на недефинираните коефициенти

Същността на метода е, че първоначалният полином се разлага на фактори с неизвестни коефициенти. Използвайки свойството, че полиномите са равни, ако техните коефициенти са равни при същите градуси, се откриват неизвестните коефициенти на разширение.

Пример 1.

x 3 + 4x 2 + 5x + 2 = 0.

Решение.

Полином от 3-та степен може да бъде разложен на произведение на линеен и квадратен фактор.

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

След като реших системата:

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(а = -1,
(b = 3,
(c = 2, т.е.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

Корените на уравнението (x + 1) (x 2 + 3x + 2) = 0 са лесни за намиране.

Отговор: -1; -2.

4. Метод за избор на корена по най-високия и свободния коефициент

Методът се основава на прилагането на теореми:

1) Всеки целочислен корен от полином с цели коефициенти е делител на свободния член.

2) За да може несводимата дроб p / q (p е цяло число, q е естествено число) да бъде корен на уравнение с цели коефициенти, е необходимо числото p да е целочислен делител на свободния член a 0, и q - естествен делител на водещия коефициент.

Пример 1.

6x 3 + 7x 2 - 9x + 2 = 0.

Решение:

6: q = 1, 2, 3, 6.

Следователно p / q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6.

След като намерим един корен, например - 2, намираме други корени, използвайки деление с ъгъл, метода на неопределените коефициенти или схемата на Хорнер.

Отговор: -2; 1/2; 1/3.

Все още имате въпроси? Не сте сигурни как да решавате уравнения?
За да получите помощ от преподавател - регистрирайте се.
Първият урок е безплатен!

сайт, с пълно или частично копиране на материала, е необходима връзка към източника.

В youtube канала на нашия сайт, за да сте в течение на всички нови видео уроци.

За начало нека си припомним основните формули за степени и техните свойства.

Продукт на число асе случва на себе си n пъти, можем да запишем този израз като a a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Мощност или експоненциални уравнения - това са уравнения, в които променливите са в степени (или експоненти), а основата е число.

Примери за експоненциални уравнения:

V този примерчислото 6 е основата, то винаги стои на дъното и променливата хстепен или индикатор.

Ето още няколко примера за експоненциални уравнения.
2 х * 5 = 10
16 x - 4 x - 6 = 0

Сега нека разгледаме как се решават експоненциалните уравнения?

Да вземем едно просто уравнение:

2 х = 2 3

Такъв пример може да бъде решен дори в ума. Вижда се, че х = 3. В крайна сметка, за да са равни лявата и дясната страна, трябва да поставите числото 3 вместо x.
Сега нека видим как това решение трябва да бъде формализирано:

2 х = 2 3
х = 3

За да решим такова уравнение, ние го премахнахме идентични основания(тоест двойки) и написах каквото е останало, това са степени. Получихме желания отговор.

Сега нека обобщим нашето решение.

Алгоритъм за решаване на експоненциалното уравнение:
1. Трябва да се провери същотодали уравнението има основи отдясно и отляво. Ако основанията не са еднакви, търсим варианти за решаване на този пример.
2. След като основите са еднакви, приравняватстепен и решете полученото ново уравнение.

Нека сега решим няколко примера:

Да започнем просто.

Основите от лявата и дясната страна са равни на числото 2, което означава, че можем да изхвърлим основата и да изравним техните степени.

x + 2 = 4 Това е най -простото уравнение.
х = 4 - 2
х = 2
Отговор: x = 2

В следващия пример можете да видите, че основите са различни, те са 3 и 9.

3 3x - 9x + 8 = 0

Като начало, прехвърляме деветката в дясната страна, получаваме:

Сега трябва да направите същите основи. Знаем, че 9 = 3 2. Нека използваме формулата за степени (a n) m = a nm.

3 3x = (3 2) x + 8

Получаваме 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 сега можете да видите, че основите от лявата и дясната страна са еднакви и равни на три, така че можем да ги изхвърлим и да изравним степените.

3x = 2x + 16 получава най-простото уравнение
3x - 2x = 16
х = 16
Отговор: x = 16.

Вижте следния пример:

2 2x + 4 - 10 4 x = 2 4

На първо място, ние разглеждаме основите, основите са различни две и четири. И ние имаме нужда те да бъдат еднакви. Преобразувайте четирите по формулата (a n) m = a nm.

4 x = (2 2) x = 2 2x

Използваме и една формула a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Добавете към уравнението:

2 2x 2 4 - 10 2 2x = 24

Доведохме примера до същите основания. Но ни пречат други числа 10 и 24. Какво да правим с тях? Ако се вгледате внимателно, можете да видите, че от лявата страна повтаряме 2 2x, ето отговора - 2 2x можем да извадим от скобите:

2 2x (2 4 - 10) = 24

Нека изчислим израза в скоби:

2 4 — 10 = 16 — 10 = 6

Разделете цялото уравнение на 6:

Нека си представим 4 = 2 2:

2 2x = 2 2 основи са еднакви, изхвърляме ги и приравняваме степените.
2x = 2 получаваме най -простото уравнение. Разделяме го на 2, получаваме
x = 1
Отговор: х = 1.

Нека решим уравнението:

9 x - 12 * 3 x + 27 = 0

Нека трансформираме:
9 x = (3 2) x = 3 2x

Получаваме уравнението:
3 2x - 12 3x +27 = 0

Нашите основи са еднакви, равни на 3. В този пример можете да видите, че първите три имат степен два пъти (2x) от втората (само x). В този случай можете да решите метод на подмяна... Заменете числото с най-малката степен:

Тогава 3 2x = (3x) 2 = t 2

Заменете всички степени с x в уравнението с t:

t 2 - 12t + 27 = 0
Получаваме квадратно уравнение. Решаваме чрез дискриминанта, получаваме:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Връщане към променливата х.

Вземаме t 1:
t 1 = 9 = 3 x

Това е,

3 х = 9
3 х = 3 2
x 1 = 2

Намерен е един корен. Търсим втория, от t 2:
t 2 = 3 = 3 x
3 х = 3 1
х 2 = 1
Отговор: x 1 = 2; x 2 = 1.

На сайта можете в секцията ПОМОГНЕТЕ ЗА РЕШЕНИЕТОза да зададете въпроси, представляващи интерес, ние определено ще ви отговорим.

Присъединете се към групата

Съдейки по началото на публикацията, която пропускаме тук, текстът е написан от Юрий Игнатиевич. И е написано добре, а проблемът е актуален, това е единственият начин да се обадим на Русия, както прави Мухин ...

Без значение как някой се отнася към антинародната власт, Русия е над нея и не заслужава обиди. Дори от талантливия осведомител на американската агенция НАСА.

*

Обръщение към другарю Мухин Ю.И.

Уважаеми Юрий Игнатиевич!Знам, че посещавате тези страници. Затова се обръщам директно към вас.

Всички оценяваме вашата безкористна работа в областта на разобличаването на лъжите на Запада, лъжите на Америка, лъжите на псевдоучените и лъжите на либералите. С удоволствие и полза за себе си и обществото, ние мислим за сериозни теми, които ни подхвърляте от време на време, било то меритокрация или метафизика, любов към национална историяили възстановяване на справедливостта.

Вашите определения за общата ни родина обаче са недоумяващи и много смущаващи.

Преценете обаче сами: как бихте характеризирали човек, който започна да обижда майка си, която беше болна и временно спря да работи поради това?

Но Русия, без значение как се нарича, и колкото и добро или отвратително да е правителството, Русия е нашата Родина. Родина.За нея нашите дядовци проляха кръв и дадоха живота си.

Следователно поставянето му наравно със силата означава снижаване на духовното възвишено до нивото на материалното и дори ниско. Тези. сравнявате напълно различни категории. Нещо, което е неприемливо за всеки здравомислещ човек.

Питам те, драги другарю. Мухин, помислете сериозно за това.

**

... А с уравненията (аз не знаех това) положението е следното. Как да намерим корени квадратно уравнениесе предполага още в древен Египет.

Как да се намерят корените на кубичното уравнение и уравнението от четвърта степен е открито през шестнадесети век, но те не могат да намерят корените на уравнението от пета степен до 2016 г. И далеч от обикновените хора се опитаха.

През шестнадесети век основателят на символната алгебра Франсоа Виет се опитва да намери корените на уравнението от пета степен; през деветнадесети век основателят на съвременната висша алгебра, френският математик Еварист Галоа, се опитва да намери корените на уравненията от пета степен; след него норвежкият математик Нилс Хенрик Абел се опита да се откаже и доказа невъзможността за решаване на уравнение от пета степен в общ изглед.

В Уикипедия четем за достойнствата на Абел: „Абел завърши брилянтно изследване на древен проблем:доказа невъзможността да се реши в общ вид (в радикали) уравнението от 5-та степен ...

В алгебрата Абел намира необходимото условие коренът на уравнението да бъде изразен "в радикали" по отношение на коефициентите на това уравнение. Достатъчното условие скоро е открито от Галоа, чиито постижения се основават на произведенията на Авел.

Абел даде конкретни примери за уравнение от 5-та степен, чиито корени не могат да бъдат изразени в радикали, и по този начин до голяма степен затвори древния проблем."

Както виждате, ако те се опитваха да докажат теоремата на Поанкаре през цялото време и Перелман се оказа по-щастлив от останалите математици, то след Абел математиците не се заеха с уравненията от пета степен.

И през 2014г математик от Томск Сергей Зайков, за когото по снимката може да се съди, че вече е на години, а по данните от статията за него, че е възпитаник на факултета приложна математикаи кибернетиката на Томск държавен университет, в хода на работата си получава уравнения от пета степен. Задънен край? Да, задънена улица! Но Сергей Зайков се зае да го разбие.

И през 2016 г. той намери начини за решаване на уравнения от пета степен в общ вид! Той направи това, което математиците Галоа и Абел се оказаха невъзможно.

Опитах се да намеря информация за Сергей Зайков в Уикипедия, но майната му! За математика Сергей Зайков и за неговото намиране на решение на уравнения от пета степен няма информация!

Фактът, че за математиците има аналог на Нобелова награда -награда Абел(Нобел забрани да се дава наградата на математиците и сега тя се дава за математически изпражнения, наричайки ги „физика“).

Тази математическа награда е в чест на самия Авел, който доказа невъзможността на това, което е направил Зайков... Самономинирането за тази награда обаче не е разрешено. А Зайков е самотен математик и няма организации, които биха могли да го предложат за кандидат за тази награда.

Вярно е, че имаме Академия на науките, но в края на краищата академиците не седят там за развитието на математиката, а „за да режат плячката“. Кому е нужен този Зайков там?

Е, за информационните агенции Зайков не е Перелман за вас! Затова откритието на Зайков за медиите не е сензация.

Че Порошенко сбърка с вратата - да! Това е истинска сензация!

Томският математик реши проблем, който не можеше да бъде решен двеста години

С появата на алгебрата решаването на алгебрични уравнения се счита за основна задача. Решението на уравнение от втора степен вече беше известно във Вавилон и Древен Египет... Преминаваме през такива уравнения в училище. Помните ли уравнението x2 + ax + b = 0 и дискриминанта?

Сергей Зайков с книга

Решението на алгебричните уравнения от трета и четвърта степен е намерено през шестнадесети век. Но не беше възможно да се реши уравнението от пета степен. Причината е открита от Лагранж. Той показа, че решението на уравнения от трета и четвърта степен става възможно, тъй като те могат да бъдат сведени до уравнения, които вече са решени. Уравнение от трета степен може да бъде намалено до уравнение от втора степен, а уравнение от четвърта до уравнение от трета. Но уравнението от пета степен се свежда до уравнението на шестата, тоест по-сложно, следователно традиционните методи за решаване не са приложими.

Въпросът за решаването на уравнение от пета степен се премести само преди двеста години, когато Абел доказа, че не всички уравнения от пета степен могат да бъдат решени в радикали, тоест в квадратни, кубични и други корени, известни ни от училище. И скоро Галуа, тоест преди двеста години, намери критерий за определяне кои уравнения от пета степен могат да бъдат решени в радикали и кои не. Той се състои в това, че групата на Галуа, разрешима в радикали на уравнение от пета степен, трябва да бъде или циклична, или метациклична. Но Галоа не намери начин да реши в радикали онези уравнения от пета степен, които са разрешими в радикали. Теорията на Галоа е много известна, много книги са написани за нея.

Досега са открити само конкретни решения за уравнения от пета степен, разрешими в радикали. И едва тази година Томският математик Сергей Зайков реши проблем, който не можеше да бъде решен в продължение на двеста години. Издаде книгата „Как се решават те в радикали? алгебрични уравненияпета степен“, в която той посочи метод за решаване на всякакви уравнения от пета степен, които са разрешими в радикали. Зайков е завършил Факултета по приложна математика и кибернетика на Томския държавен университет. Успяхме да го интервюираме.

- Сергей, защо започна да решаваш този проблем?

- Трябваше да реша уравнение от пета степен, за да реша задача от друг клон на математиката. Започнах да измислям как да го намеря и установих, че не всички са решени в радикали. Тогава се опитах да потърся научна литератураметод за решаване на онези уравнения, които са разрешими в радикали, но намира само критерий, по който може да се определи кои са разрешими и кои не. Не съм алгебраист, но, разбира се, като завършил ФПМК, мога да прилагам и алгебрични методи. Затова от 2014 г. започнах сериозно да търся решение и сам го намерих.

Методът беше открит от мен преди две години, подготвих книга, в която не само беше описан, но и начини за решаване на някои уравнения на степени по -големи от петата. Но нямах пари да го публикувам. Тази година реших, че ще бъде по -лесно да публикувам само част от тази работа и взех само половината от нея, посветена на начина за решаване на уравнението на петата степен в радикалите.

Поставих си за цел да публикувам нещо като ръководство за решаване на този проблем, разбираемо за математиците, които трябва да решат конкретно уравнение. Затова го опростих, като премахнах много дълги формулии голяма част от теорията, съкращавайки повече от половината, оставяйки само най-важното. Затова в крайна сметка получих нещо като книга „за манекени“, според която математиците, които не са запознати с теорията на Галоа, могат да решат уравнението, от което се нуждаят.

- За това много благодаря на Владислав Береснев, с когото се познаваме от много години. Той спонсорира издаването на книгата.

- Възможно ли е да получите някаква награда по математика за решаване на този проблем? Например споменахте Абел. Но има ли Абелова награда по математика, която се смята за аналог на Нобеловата награда?

- Тази възможност не може да бъде напълно изключена. Но и вие не трябва да се надявате на това.

Например заявленията за кандидати за наградата Абел за 2019 г. трябва да бъдат подадени до 15 септември. Освен това самономинацията не е разрешена. И аз съм самотен математик. Няма организации или известни математици, които да ме номинират. Следователно няма да се разглежда, независимо дали работата ми заслужава тази награда и дали е в духа на тази награда да я присъдим на онези, които продължават делото на Авел. Но дори и да бъде представен, всичко зависи и от нивото на работа на другите кандидати.

Книгата е предназначена за тези, които не са запознати с теорията на Галоа. Основите на теорията на Галоа са дадени само в частта, в която са необходими за решаването на уравнението, методът на решението е описан подробно и са показани техники, които опростяват решението. Голяма част от книгата е посветена на примера за решаване на конкретно уравнение. Рецензенти на книгата са доктор на техническите науки Генадий Петрович Агибалов и доктор по физика. мат. наук, професор Петр Андреевич Крилов.

ПОДГОТОВЕН АНАСТАСИЯ СКИРНЕВСКАЯ