Rovnica kruhu. Rovnica kruhu. Vysvetlenie nového materiálu
Účel lekcie: zaviesť rovnicu kruhu, naučiť žiakov vytvárať rovnicu kruhu podľa hotového nákresu, postaviť kruh podľa danej rovnice.
Zariadenie: interaktívna tabuľa.
Plán lekcie:
- Organizačný moment - 3 min.
- Opakovanie. Organizácia duševnej činnosti - 7 min.
- Vysvetlenie nového materiálu. Odvodenie rovnice kruhu - 10 min.
- Spevnenie študovaného materiálu - 20 min.
- Zhrnutie lekcie - 5 min.
Počas vyučovania
2. Opakovanie:
− (Príloha 1 Snímka 2) zapíšte si vzorec na nájdenie súradníc stredu segmentu;
− (Snímka 3) W Napíšte vzorec vzdialenosť medzi bodmi (dĺžka segmentu).
3. Vysvetlenie nového materiálu.
(Snímky 4 - 6) Uveďte definíciu rovnice kruhu. Odvodte rovnice kruhu so stredom v bode ( a;b) a vycentrovaný v počiatku.
(NS – a ) 2 + (o – b ) 2 = R. 2 - rovnica kruhu so stredom S (a;b) , polomer R. , NS a o – súradnice ľubovoľného bodu kruhu .
NS 2 + y 2 = R. 2 - rovnica kruhu so stredom na začiatku.
(Snímka 7)
Na zostavenie rovnice kruhu potrebujete:
- poznať súradnice stredu;
- poznať dĺžku polomeru;
- nahraďte stredové súradnice a dĺžku polomeru v rovnici kruhu.
4. Riešenie problémov.
V úlohách č.1 - č.6 zostavte rovnice kruhu podľa hotových výkresov.



(Snímka 14)
№ 7. Vyplňte tabuľku.

(Snímka 15)
№ 8. Zostrojte kruhy v zošite dané rovnicami:
a) ( NS – 5) 2 + (o + 3) 2 = 36;
b) (NS + 1) 2 + (o– 7) 2 = 7 2 .
(Snímka 16)
№ 9. Nájdite súradnice stredu a dĺžku polomeru if AB Je priemer kruhu.
| Vzhľadom na to: | Riešenie: | ||
| R. | Stredové súradnice | ||
| 1 | A(0 ; -6) V.(0 ; 2) |
AB 2 = (0 – 0) 2 + (2 + 6) 2 ; AB 2 = 64; AB = 8 . |
A(0; -6) V.(0 ; 2) S(0 ; – 2) – Stred |
| 2 | A(-2 ; 0) V.(4 ; 0) |
AB 2 = (4 + 2) 2 + (0 + 0) 2 ; AB 2 = 36; AB = 6. |
A (-2;0) V. (4 ;0) S(1 ; 0) – Stred |
(Snímka 17)
№ 10. Rovnaký kruh ako stred v počiatku prechádzajúci bodom TO(-12;5).
Riešenie.
R 2 = OK 2
= (0 + 12) 2 +
(0 – 5) 2 = 144 + 25 = 169;
R = 13;
Kruhová rovnica: x 2 + y 2 = 169 .
(Snímka 18)
№ 11. Prirovnajte kružnicu cez začiatok so stredom v bode S(3; - 1).
Riešenie.
R2= OS 2 = (3 – 0) 2 + (–1–0) 2 = 9 + 1 = 10;
Kruhová rovnica: ( NS - 3) 2 + (y + 1) 2 = 10.
(Snímka 19)
№ 12. Zarovnajte kruh so stredom A(3; 2) prechádzajúci V.(7;5).
Riešenie.
1. Stred kruhu - A(3;2);
2.R. = AB;
AB 2 = (7 – 3) 2 + (5 – 2) 2 = 25; AB
= 5;
3. Rovnica kruhu ( NS – 3) 2 + (o − 2) 2
= 25.
(Snímka 20)
№ 13. Skontrolujte, či body ležia A(1; -1), V.(0;8), S(-3; -1) na kružnici definovanej rovnicou ( NS + 3) 2 + (o − 4) 2 = 25.
Riešenie.
Ja... Dosaďte súradnice bodu A(1; -1) do rovnice kruhu:
(1 + 3) 2 +
(−1 − 4) 2 =
25;
4 2 + (−5) 2 = 25;
16 + 25 = 25;
41 = 25 - rovnosť je nesprávna, takže A(1; -1) neklame v kruhu danom rovnicou ( NS + 3) 2 +
(o −
4) 2 =
25.
II... Dosaďte súradnice bodu V.(0; 8) do rovnice kruhu:
(0 + 3) 2 +
(8 − 4) 2 =
25;
3 2 + 4 2 = 25;
9 + 16 = 25;
V.(0;8)lži NS + 3) 2 +
(o − 4) 2
=
25.
III. Dosaďte súradnice bodu S(-3; -1) do rovnice kruhu:
(−3 + 3) 2 +
(−1− 4) 2 =
25;
0 2 + (−5) 2 = 25;
25 = 25 - rovnosť je pravdivá, takže S(-3; -1) lži na kružnici danej rovnicou ( NS + 3) 2 +
(o − 4) 2
=
25.
Zhrnutie lekcie.
- Recenzia: Rovnica kruhu, Rovnica kruhu so stredom na začiatku.
- (Snímka 21) Domáca úloha.
Definícia 1. Číselná os ( číselný riadok, súradnicový riadok) Vola sa nazýva priama čiara, na ktorej je vybraný bod O pôvod (pôvod)(obr. 1), smer
O → X
označené ako pozitívny smer a je označený segment, ktorého dĺžka sa berie ako jednotka dĺžky.


Definícia 2. Segment, ktorého dĺžka sa berie ako jednotka dĺžky, sa nazýva mierka.
Každý bod numerickej osi má súradnicu, ktorá je Reálne číslo... Súradnica bodu O je nulová. Súradnica ľubovoľného bodu A ležiaceho na lúči Ox sa rovná dĺžke úsečky OA. Súradnica ľubovoľného bodu A číselnej osi, ktorý neleží na lúči Ox, je záporná av absolútnej hodnote sa rovná dĺžke segmentu OA.
Definícia 3. Pravouhlý karteziánsky súradnicový systém Oxy v rovine zavolajte dvoch navzájom kolmýčíselné osi Ox a Oy s rovnakej mierke a spoločný referenčný bod v bode O a také, že rotácia z lúča Ox v uhle 90 ° k lúču Oy sa vykonáva v smere proti smeru hodinových ručičiek(obr. 2).


Poznámka. Nazýva sa pravouhlý karteziánsky súradnicový systém Oxy, znázornený na obrázku 2 správny súradnicový systém, Na rozdiel od ľavé súradnicové systémy, v ktorom sa otáčanie lúča Ox pod uhlom 90 ° k lúču Oy vykonáva v smere hodinových ručičiek. V tejto príručke sme zvážiť iba pravotočivé súradnicové systémy bez uvedenia.
Ak do roviny zavedieme nejaký systém pravouhlých karteziánskych súradníc Oxy, potom každý bod roviny nadobúda dve súradnice – úsečka a ordinovať, ktoré sa vypočítajú nasledovne. Nech A je ľubovoľný bod roviny. Zhodme kolmice z bodu A AA 1 a AA 2 k čiaram Ox a Oy (obr. 3).


Definícia 4. Rovnica bodu A je súradnica bodu A 1 na číselnej osi Ox je súradnica bodu A súradnica bodu A 2 na číselnej osi Oy.
Označenie. Súradnice bodu (osa x) A v obdĺžnikovej karteziánskej súradnicovej sústave Oxy (obr. 4) sa zvyčajne označuje A(X;r) alebo A = (X; r).
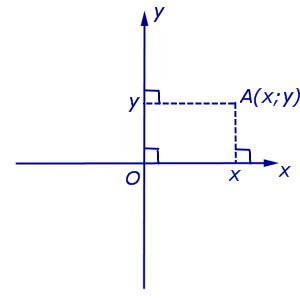

Poznámka. Bod O volal pôvod, má súradnice O(0 ; 0) .
Definícia 5. V pravouhlom karteziánskom súradnicovom systéme Oxy číselná os Ox sa nazýva súradnicová os a číselná os Oy sa nazýva ordináta (obr. 5).
Definícia 6. Každý pravouhlý karteziánsky súradnicový systém rozdeľuje rovinu na 4 štvrtiny (kvadranty), ktorých číslovanie je znázornené na obrázku 5.


Definícia 7. Nazýva sa rovina, na ktorej je zadaný pravouhlý karteziánsky súradnicový systém súradnicová rovina.
Poznámka. Os x je nastavená na súradnicová rovina rovnica r= 0, zvislá os je určená v rovine súradníc rovnicou X = 0.
Vyhlásenie 1. Vzdialenosť medzi dvoma bodmi súradnicová rovina
A 1 (X 1 ;r 1) a A 2 (X 2 ;r 2)
vypočítané podľa vzorca
Dôkaz . Zvážte obrázok 6.


Obvod nazývaná množina bodov roviny, v rovnakej vzdialenosti od daného bodu, nazývaná stred.
Ak je bod C stredom kruhu, R je jeho polomer a M je ľubovoľný bod kruhu, potom podľa definície kruhu
Rovnosť (1) je kruhová rovnica polomer R so stredom v bode C.
Nech pravouhlý karteziánsky súradnicový systém (obr. 104) a bod C ( a; b) je stred kružnice s polomerom R. Nech M ( NS; o) je ľubovoľný bod tohto kruhu.
Pretože | CM | = \ (\ sqrt ((x - a) ^ 2 + (y - b) ^ 2) \), potom rovnicu (1) možno zapísať takto:
\ (\ sqrt ((x - a) ^ 2 + (y - b) ^ 2) \) = R
(x - a) 2 + (y - b)2 = R2 (2)
Rovnica (2) sa nazýva všeobecná rovnica kruhu alebo rovnica kružnice s polomerom R so stredom v bode ( a; b). Napríklad rovnica
(X - l) 2 + ( r + 3) 2 = 25
je rovnica kruhu s polomerom R = 5 so stredom v bode (1; -3).
Ak sa stred kruhu zhoduje s počiatkom, potom rovnica (2) nadobúda tvar
X 2 + o 2 = R2. (3)
Rovnica (3) sa nazýva kanonická rovnica kruhu .
Cieľ 1. Napíšte rovnicu kruhu s polomerom R = 7 so stredom na začiatku.
Priamym nahradením hodnoty polomeru do rovnice (3) získame
X 2 + o 2 = 49.
Cieľ 2. Napíšte rovnicu kružnice s polomerom R = 9 so stredom v bode C (3; -6).
Nahradením hodnoty súradníc bodu C a hodnoty polomeru do vzorca (2) získame
(NS - 3) 2 + (o- (-6)) 2 = 81 alebo ( NS - 3) 2 + (o + 6) 2 = 81.
Cieľ 3 Nájdite stred a polomer kruhu
(NS + 3) 2 + (o-5) 2 =100.
Porovnaním tejto rovnice so všeobecnou rovnicou kruhu (2) to vidíme a = -3, b= 5, R = 10. Preto C (-3; 5), R = 10.
Úloha 4. Dokážte, že rovnica
X 2 + o 2 + 4NS - 2r - 4 = 0
je rovnica kruhu. Nájdite jeho stred a polomer.
Transformujeme ľavú stranu tejto rovnice:
X 2 + 4NS + 4- 4 + o 2 - 2o +1-1-4 = 0
(NS + 2) 2 + (o - 1) 2 = 9.
Táto rovnica je rovnicou kruhu so stredom v bode (-2; 1); polomer kruhu je 3.
Úloha 5. Napíšte rovnicu kružnice so stredom v bode C (-1; -1), dotyčnice k priamke AB, ak A (2; -1), B (- 1; 3).
Napíšme rovnicu priamky AB:
![]() alebo 4 NS + 3r-5 = 0.
alebo 4 NS + 3r-5 = 0.
Pretože sa kružnica dotýka tejto priamky, polomer nakreslený k dotyčnicovému bodu je kolmý na túto priamku. Ak chcete nájsť polomer, musíte nájsť vzdialenosť od bodu C (-1; -1) - stredu kruhu k priamke 4 NS + 3r-5 = 0:
Napíšme rovnicu požadovaného kruhu
(X +1) 2 + (r +1) 2 = 144 / 25
Nech je daný kruh v pravouhlom súradnicovom systéme X 2 + o 2 = R2. Zvážte jeho ľubovoľný bod M ( NS; o) (obr. 105).

Nechajte vektor polomeru OM> bod M tvorí uhol veľkosti t s kladným smerom osi O NS, potom sa os x a súradnica bodu M menia v závislosti od t
(0 t x a y cez t, nachádzame
X= R cos t ; r= R hriech t , 0 t
Rovnice (4) sa nazývajú parametrické rovnice kruhu so stredom na začiatku.
Úloha 6. Kruh je daný rovnicami
X= \ (\ sqrt (3) \) cos t, r= \ (\ sqrt (3) \) hriech t, 0 t
Napíšte kanonickú rovnicu pre tento kruh.
Podmienka znamená X 2 = 3 ako 2 t, o 2 = 3 hriechy 2 t... Sčítaním týchto rovností po členoch získame
X 2 + o 2 = 3 (cos 2 t+ hriech 2 t)
alebo X 2 + o 2 = 3
Nech má kruh polomer  a jeho stred je v bode
a jeho stred je v bode  ... Bod
... Bod  leží na kružnici práve vtedy, ak modul vektora
leží na kružnici práve vtedy, ak modul vektora  rovná sa
rovná sa  , teda. Posledná rovnosť platí vtedy a len vtedy
, teda. Posledná rovnosť platí vtedy a len vtedy
Rovnica (1) je požadovaná rovnica kruhu.
Rovnica priamky prechádzajúcej daným bodom, kolmá na daný vektor
 kolmo na vektor
kolmo na vektor  .
.

Bod 
 a
a  kolmý. vektory
kolmý. vektory  a
a  sú kolmé práve vtedy, ak je ich bodový súčin nula
sú kolmé práve vtedy, ak je ich bodový súčin nula  ... Pomocou vzorca na výpočet skalárneho súčinu vektorov daného ich súradnicami zapíšeme rovnicu požadovanej priamky v tvare
... Pomocou vzorca na výpočet skalárneho súčinu vektorov daného ich súradnicami zapíšeme rovnicu požadovanej priamky v tvare
Pozrime sa na príklad. Nájdite rovnicu, ktorou priamka prechádza
stred segmentu AB je kolmý na tento segment, ak sú súradnice bodov zodpovedajúce A (1; 6), B (5; 4).
Budeme argumentovať nasledovne. Aby sme našli rovnicu priamky, musíme poznať bod, ktorým táto čiara prechádza, a vektor kolmý na túto priamku. Vektor kolmý na danú čiaru bude vektorom, pretože podľa tvrdenia o probléme je čiara kolmá na segment AB. Bod  definujte z podmienky, že priamka prechádza stredným AB. Máme. Teda
definujte z podmienky, že priamka prechádza stredným AB. Máme. Teda  a rovnica má tvar.
a rovnica má tvar.
Ujasnime si otázku, či táto priamka prechádza bodom M (7; 3).
Máme teda, táto priamka neprechádza zadaným bodom.
Rovnica priamky prechádzajúcej daným bodom rovnobežne s daným vektorom
Nechajte čiaru prejsť bodom  paralelne s vektorom
paralelne s vektorom  .
.

Bod  leží na priamke práve vtedy, ak vektory
leží na priamke práve vtedy, ak vektory  a
a  kolineárne. vektory
kolineárne. vektory  a
a  kolineárne vtedy a len vtedy, ak sú ich súradnice proporcionálne, tj
kolineárne vtedy a len vtedy, ak sú ich súradnice proporcionálne, tj
 (3)
(3)
Výsledná rovnica je rovnicou požadovanej priamky.
Rovnica (3) môže byť reprezentovaná ako
 , kde
, kde  má akékoľvek hodnoty
má akékoľvek hodnoty  .
.
Preto môžeme písať
 , kde
, kde  (4)
(4)
Sústavu rovníc (4) nazývame parametrické rovnice priamky.
Pozrime sa na príklad. Nájdite rovnicu priamky prechádzajúcej bodmi. Rovnicu priamky môžeme zostrojiť, ak poznáme bod a vektor rovnobežný alebo kolmý na neho. K dispozícii sú až dva body. Ale ak dva body ležia na priamke, potom vektor, ktorý ich spája, bude rovnobežný s touto priamkou. Preto používame rovnicu (3), pričom vezmeme ako vektor  vektor
vektor  ... Dostaneme
... Dostaneme
 (5)
(5)
Rovnica (5) sa nazýva rovnica priamky prechádzajúcej dvoma danými bodmi.
Všeobecná rovnica priamky
Definícia. Všeobecná rovnica priamky prvého rádu na rovine je rovnicou tvaru  , kde
, kde  .
.
Veta. Akákoľvek priamka v rovine môže byť daná vo forme rovnice priamky prvého rádu a každá rovnica priamky prvého rádu je rovnicou nejakej priamky v rovine.
Prvá časť tejto vety sa dá ľahko dokázať. Na ľubovoľnej priamke môžete určiť nejaký bod  vektor naň kolmý
vektor naň kolmý  ... Potom podľa (2) rovnica takejto priamky má tvar. Označujeme
... Potom podľa (2) rovnica takejto priamky má tvar. Označujeme  ... Potom rovnica nadobudne tvar
... Potom rovnica nadobudne tvar  .
.
Teraz prejdeme k druhej časti vety. Nech existuje rovnica  , kde
, kde  ... Pre istotu predpokladáme
... Pre istotu predpokladáme  .
.
Prepíšme rovnicu takto:
 ;
;
V lietadle zvážte bod  , kde
, kde  ... Výsledná rovnica má potom tvar a je rovnicou priamky prechádzajúcej bodom
... Výsledná rovnica má potom tvar a je rovnicou priamky prechádzajúcej bodom  kolmo na vektor
kolmo na vektor  ... Veta je dokázaná.
... Veta je dokázaná.
V priebehu dokazovania vety sme na ceste dokázali
Vyhlásenie. Ak existuje priama rovnica tvaru  , potom vektor
, potom vektor  kolmo na túto priamku.
kolmo na túto priamku.
Rovnica tvaru
 sa nazýva všeobecná rovnica priamky v rovine.
sa nazýva všeobecná rovnica priamky v rovine.
Nech je rovná čiara  a bod
a bod  ... Je potrebné určiť vzdialenosť od určeného bodu k priamke.
... Je potrebné určiť vzdialenosť od určeného bodu k priamke.
Zvážte svojvoľný bod  na priamke. Máme
na priamke. Máme  ... Vzdialenosť
... Vzdialenosť  z bodu
z bodu  na priamku sa rovná modulu vektorového premietania
na priamku sa rovná modulu vektorového premietania  na vektor
na vektor  kolmo na túto čiaru. Máme
kolmo na túto čiaru. Máme
 ,
,
transformácia, dostaneme vzorec:

Nech sú dané dve rovné čiary dané všeobecnými rovnicami
 ,
,
 ... Potom vektory
... Potom vektory 
 sú kolmé na prvú a druhú priamku. Injekcia
sú kolmé na prvú a druhú priamku. Injekcia  medzi rovnými rovný uhlu medzi vektormi
medzi rovnými rovný uhlu medzi vektormi  ,
, .
.
Potom vzorec na určenie uhla medzi rovnými čiarami je:
 .
.
Podmienka kolmosti priamych čiar je nasledovná:
 .
.
Čiary sú rovnobežné alebo sa zhodujú práve vtedy, ak sú vektory 
 kolineárne. Kde podmienka zhody priamok má tvar:
kolineárne. Kde podmienka zhody priamok má tvar:
 ,
,
a podmienka neprítomnosti križovatky je napísaná takto:
 ... Posledné dve podmienky dokážte sami.
... Posledné dve podmienky dokážte sami.
Preskúmajme povahu správania sa priamky podľa jej všeobecnej rovnice.
Nech je to dané všeobecná rovnica rovno  ... Ak
... Ak  , potom priamka prechádza počiatkom.
, potom priamka prechádza počiatkom.
Zvážte prípad, keď žiadny z koeficientov nie je rovný nule  ... Rovnicu prepíšeme do tvaru:
... Rovnicu prepíšeme do tvaru:
 ,
,
 ,
,
Kde  ... Poďme zistiť význam parametrov
... Poďme zistiť význam parametrov  ... Nájdite priesečníky priamky so súradnicovými osami. O
... Nájdite priesečníky priamky so súradnicovými osami. O  máme
máme  , a na
, a na  máme
máme  ... To je
... To je  sú segmenty, ktoré sú odrezané priamkou na súradnicových osiach. Preto rovnica
sú segmenty, ktoré sú odrezané priamkou na súradnicových osiach. Preto rovnica
 sa nazýva rovnica priamky v segmentoch.
sa nazýva rovnica priamky v segmentoch.

Kedy  máme
máme 
 ... Kedy
... Kedy  máme
máme  ... To znamená, že priama čiara bude rovnobežná s osou
... To znamená, že priama čiara bude rovnobežná s osou  .
.
Pripomeňme si to sklon priamky
 nazývaná dotyčnica uhla sklonu tejto priamky k osi
nazývaná dotyčnica uhla sklonu tejto priamky k osi  ... Nechajte čiaru odrezať na osi
... Nechajte čiaru odrezať na osi  sekcii
sekcii  a má sklon
a má sklon  ... Nechajte vec
... Nechajte vec  klame s týmto
klame s týmto

Potom  =
= =
= ... A rovnica priamky bude napísaná vo forme
... A rovnica priamky bude napísaná vo forme
 .
.
Nechajte čiaru prejsť bodom  a má sklon
a má sklon  ... Nechajte vec
... Nechajte vec  leží na tejto priamke.
leží na tejto priamke.

Potom  =
= .
.
Výsledná rovnica sa nazýva rovnica priamky prechádzajúcej daným bodom s daným sklonom.
Dané dva riadky  ,
, ... Označujeme
... Označujeme  - uhol medzi nimi. Nechaj byť
- uhol medzi nimi. Nechaj byť  ,
, uhly sklonu k osi X zodpovedajúcich priamok
uhly sklonu k osi X zodpovedajúcich priamok

Potom  =
=
 ,
, .
.
Potom má podmienka rovnobežnosti priamok tvar  a podmienka kolmosti
a podmienka kolmosti

Na záver zvážime dve úlohy.
Úloha ... Vrcholy trojuholníka ABC majú súradnice: A (4; 2), B (10; 10), C (20; 14).
Nájdite: a) rovnicu a dĺžku mediánu nakreslenú z vrcholu A;
b) rovnica a dĺžka výšky ťahanej zhora A;
c) rovnica úsečky odvodená z vrcholu A;

Definujme rovnicu mediánu AM.
Bod М () je stredom segmentu BC.
Potom ![]() ,
,
![]() ... V dôsledku toho má bod M súradnice M (15; 17). Mediánová rovnica v jazyku analytickej geometrie je rovnica priamky prechádzajúcej bodom A (4; 2) rovnobežne s vektorom = (11; 15). Potom má rovnica mediánu tvar. Stredná dĺžka AM =
... V dôsledku toho má bod M súradnice M (15; 17). Mediánová rovnica v jazyku analytickej geometrie je rovnica priamky prechádzajúcej bodom A (4; 2) rovnobežne s vektorom = (11; 15). Potom má rovnica mediánu tvar. Stredná dĺžka AM = ![]() .
.
Výšková rovnica AS je rovnica priamky prechádzajúcej bodom A (4; 2) kolmým na vektor = (10; 4). Potom je výšková rovnica 10 (x-4) +4 (y-2) = 0,5x + 2y-24 = 0.
Výška dĺžky je vzdialenosť od bodu A (4; 2) k čiare BC. Táto priamka prechádza bodom B (10; 10) rovnobežne s vektorom = (10; 4). Jeho rovnica má tvar ![]() , 2x-5r + 30 = 0. Vzdialenosť AS od bodu A (4; 2) k priamke BC sa teda rovná AS =
, 2x-5r + 30 = 0. Vzdialenosť AS od bodu A (4; 2) k priamke BC sa teda rovná AS =  .
.
Na určenie rovnice úsečky nájdeme vektor rovnobežný s touto priamkou. Využijeme na to vlastnosť kosoštvorcovej uhlopriečky. Ak z bodu A odložíme jednotkové vektory rovnako smerujúce od vektorov, potom vektor rovný ich súčtu bude rovnobežný s osou. Potom máme = +.
={6;8},
![]() ,
={16,12},
,
={16,12},
![]() .
.
Potom = ![]() Vektor = (1; 1), kolineárny k danému, môže slúžiť ako smerový vektor požadovanej priamky. Potom rovnica požadovanej priamky videla alebo x-y-2 = 0.
Vektor = (1; 1), kolineárny k danému, môže slúžiť ako smerový vektor požadovanej priamky. Potom rovnica požadovanej priamky videla alebo x-y-2 = 0.
Úloha. Rieka tečie po priamke, ktorá prechádza bodmi A (4; 3) a B (20; 11). Červená čiapočka žije v bode C (4; 8) a jej stará mama v bode D (13; 20). Každé ráno si Červená čiapočka vezme z domu prázdne vedro, ide k rieke, naberie vodu a odnesie ju k babičke. Nájdite najkratšiu cestu pre Červenú čiapočku.
Nájdeme bod E, symetrický k babke, relatívne k rieke.
Aby sme to urobili, najprv nájdeme rovnicu priamky, pozdĺž ktorej rieka tečie. Túto rovnicu možno považovať za rovnicu priamky prechádzajúcej bodom A (4; 3) rovnobežným s vektorom. Potom rovnica priamky AB má tvar.

Ďalej nájdeme rovnicu priamky DE prechádzajúcej bodom D kolmým na AB. Možno ho považovať za rovnicu priamky prechádzajúcej bodom D, kolmého na vektor  ... Máme
... Máme
Teraz nájdeme bod S - priemet bodu D na priamku AB, ako priesečník priamok AB a DE. Máme systém rovníc
 .
.
Preto má bod S súradnice S (18; 10).
Pretože S je stred segmentu DE, potom.
Podobne.
V dôsledku toho má bod E súradnice E (23; 0).
Nájdeme rovnicu priamky CE, pričom poznáme súradnice dvoch bodov tejto priamky
Bod M nájdeme ako priesečník čiar AB a CE.
Máme systém rovníc
 .
.
V dôsledku toho má bod M súradnice 
 .
.
Téma 2. Pojem rovnice povrchu v priestore. Sférická rovnica. Rovnica roviny prechádzajúcej daným bodom je kolmá tento vektor... Všeobecná rovnica roviny a jej štúdium Podmienka rovnobežnosti dvoch rovín. Vzdialenosť od bodu k rovine. Koncept rovnicovej rovnice. Rovná čiara v priestore. Kanonické a parametrické rovnice priamky v priestore. Rovnice priamky prechádzajúcej dvoma danými bodmi. Podmienky rovnobežnosti a kolmosti priamky a roviny.
Najprv poskytneme definíciu pojmu rovnica povrchu v priestore.
Pustite do priestoru  daný nejaký povrch
daný nejaký povrch  ... Rovnica
... Rovnica  sa nazýva rovnica povrchu
sa nazýva rovnica povrchu  ak sú splnené dve podmienky:
ak sú splnené dve podmienky:

1. pre akýkoľvek bod  so súradnicami
so súradnicami  ležiaci na povrchu je spokojný
ležiaci na povrchu je spokojný  , to znamená, že jeho súradnice spĺňajú rovnicu povrchu;
, to znamená, že jeho súradnice spĺňajú rovnicu povrchu;
2. akýkoľvek bod  ktorých súradnice vyhovujú rovnici
ktorých súradnice vyhovujú rovnici  , leží na trati.
, leží na trati.
