Općenito, jednadžba sa stupnjem većim od 4 ne može se riješiti u radikalima. Ali ponekad još uvijek možemo pronaći korijene polinoma s lijeve strane u jednadžbi najvišeg stupnja, ako ga predstavimo kao proizvod polinoma u stupnju najviše 4. Rješenje takvih jednadžbi temelji se na faktoringu polinoma u faktore, pa vam savjetujemo da ponovite ovu temu prije proučavanja ovog članka.

Najčešće se treba baviti jednadžbama više stepene sa celobrojnim koeficijentima. U tim slučajevima možemo pokušati pronaći racionalne korijene, a zatim umnožiti polinom kako bismo ga zatim transformirali u jednadžbu nižeg stupnja, što će biti lako riješiti. U okviru ovog materijala razmotrit ćemo upravo takve primjere.

Jednačine najvećeg stepena sa cjelobrojnim koeficijentima

Sve jednadžbe oblika a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0, možemo svesti na jednadžbu istog stepena množenjem obje strane sa a n n - 1 i promjenom varijable oblika y = a n x:

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 +… + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 +… + b 1 y + b 0 = 0

Dobijeni koeficijenti će takođe biti celi. Stoga ćemo morati riješiti reduciranu jednadžbu n -tog stupnja s cjelobrojnim koeficijentima, koja ima oblik x n + a n x n - 1 +… + a 1 x + a 0 = 0.

Izračunavamo cijele korijene jednadžbe. Ako jednadžba ima cijeli broj korijena, morate ih potražiti među djeliteljima slobodnog člana a 0. Zapišimo ih i zamijenimo ih izvornom jednakošću, provjeravajući rezultat. Kada dobijemo identitet i pronađemo jedan od korijena jednadžbe, možemo ga zapisati u obliku x - x 1 · P n - 1 (x) = 0. Ovdje je x 1 korijen jednadžbe, a P n - 1 (x) je količnik dijeljenja x n + a n x n - 1 +… + a 1 x + a 0 na x - x 1.

Zamijenite ostale djelitelje zapisane u P n - 1 (x) = 0, počevši od x 1, jer se korijeni mogu ponoviti. Nakon dobijanja identiteta, korijen x 2 smatra se pronađenim, a jednadžba se može napisati kao (x - x 1) (x - x 2) P n - 2 (x) = 0. Ovdje je P n - 2 (x) će biti količnik dijeljenja P n - 1 (x) sa x - x 2.

Nastavljamo s ponavljanjem djelitelja. Pronađite sve cijele korijene i označite njihov broj kao m. Nakon toga se originalna jednadžba može predstaviti kao x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Ovdje je P n - m (x) polinom stepena n - m. Pogodno je koristiti Hornerovu shemu za brojanje.

Ako naša izvorna jednadžba ima cjelobrojne koeficijente, ne možemo završiti s razlomačkim korijenima.

Kao rezultat toga dobili smo jednadžbu P n - m (x) = 0, čiji se korijeni mogu pronaći na bilo koji prikladan način. Mogu biti iracionalni ili složeni.

Pokažimo na konkretnom primjeru kako se takva shema rješenja primjenjuje.

Primjer 1

Stanje: pronaći rješenje jednadžbe x 4 + x 3 + 2 x 2 - x - 3 = 0.

Rešenje

Počnimo s pronalaskom cijelih korijena.

Imamo slobodan termin jednak minus tri. Ima djelitelje 1, - 1, 3 i - 3. Zamijenimo ih u originalnoj jednadžbi i vidimo koja će od njih rezultirati identitetima.

Ako je x jednako jedan, dobivamo 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, što znači da će jedan biti korijen ove jednadžbe.

Sada izvodimo dijeljenje polinoma x 4 + x 3 + 2 x 2 - x - 3 sa (x - 1) u koloni:

Dakle, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4- 1 + 3 = 0

Dobili smo identitet, što znači da smo pronašli još jedan korijen jednadžbe, jednak - 1.

Podijelite polinom x 3 + 2 x 2 + 4 x + 3 sa (x + 1) u koloni:

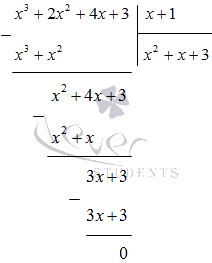
Shvatili smo to

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Zamijenite sljedeći djelitelj u jednakost x 2 + x + 3 = 0, počevši od - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Dobivene jednakosti neće biti točne, što znači da jednadžba više nema integralne korijene.

Preostali korijeni bit će korijeni izraza x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

Iz ovoga proizlazi da je dato kvadratni trinom nema pravih korijena, ali postoje složeni konjugirani: x = - 1 2 ± i 11 2.

Pojasnimo da umjesto duge podjele možemo koristiti Hornerovu shemu. To se radi ovako: nakon što odredimo prvi korijen jednadžbe, popunjavamo tablicu.

U tablici koeficijenata možemo odmah vidjeti koeficijente količnika podjele polinoma, što znači da je x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

Nakon što pronađemo sljedeći korijen jednak - 1, dobivamo sljedeće:

Odgovor: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Primjer 2

Stanje: Riješite jednadžbu x 4 - x 3 - 5 x 2 + 12 = 0.

Rešenje

Besplatni termin ima djelitelje 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

Provjeravamo ih po redoslijedu:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 ( - 1) 4 - ( - 1) 3 - 5 ( - 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Dakle, x = 2 će biti korijen jednadžbe. Podijelite x 4 - x 3 - 5 x 2 + 12 sa x - 2 pomoću Hornerove sheme:

Kao rezultat dobivamo x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Dakle, 2 će opet biti korijen. Podijelite x 3 + x 2 - 3 x - 6 = 0 sa x - 2:

Kao rezultat toga dobivamo (x - 2) 2 (x 2 + 3 x + 3) = 0.

Nema smisla provjeravati preostale djelitelje, jer je jednakost x 2 + 3 x + 3 = 0 brže i prikladnije riješiti pomoću diskriminatora.

Riješimo kvadratnu jednadžbu:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Dobijamo složeni konjugirani par korijena: x = - 3 2 ± i 3 2.

Odgovor: x = - 3 2 ± i 3 2.

Primjer 3

Stanje: pronaći prave korijene za jednadžbu x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Rešenje

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Izvodimo množenje 2 3 s obje strane jednadžbe:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Zamijenite varijable y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Na kraju smo uspjeli standardna jednadžba 4. stupanj, koji se može riješiti prema standardnoj shemi. Provjerimo djelitelje, podijelimo i na kraju zaključimo da ima 2 stvarna korijena y = - 2, y = 3 i dva složena korijena. Ovdje nećemo predstavljati cjelovito rješenje. Zbog zamjene, pravi korijeni ove jednadžbe bit će x = y 2 = - 2 2 = - 1 i x = y 2 = 3 2.

Odgovor: x 1 = - 1, x 2 = 3 2

Ako primijetite grešku u tekstu, odaberite je i pritisnite Ctrl + Enter

Razmislite rešenja jednačina sa jednom promenljivom stepena većom od druge.

Stepen jednačine P (x) = 0 je stepen polinoma P (x), tj. najveći stepen njegovih članova sa koeficijentom koji nije jednak nuli.

Tako, na primjer, jednadžba (x 3 - 1) 2 + x 5 = x 6 - 2 ima peti stupanj, jer nakon operacija otvaranja zagrada i dovođenja sličnih, dobijamo ekvivalentnu jednačinu x 5 - 2x 3 + 3 = 0 petog stepena.

Podsjetimo se pravila koja će biti potrebna za rješavanje jednadžbi stepena većeg od dva.

Tvrdnje o korijenima polinoma i njegovim djeliteljima:

1. N -ti polinom stepen ima broj korijena najviše n, a korijeni višestrukosti m javljaju se tačno m puta.

2. Polinom neparnog stepena ima najmanje jedan pravi korijen.

3. Ako je α korijen iz P (x), tada je P n (x) = (x - α) Q n - 1 (x), gdje je Q n - 1 (x) polinom stepena (n - 1).

4.

5. Reducirani polinom s cjelobrojnim koeficijentima ne može imati frakcijske racionalne korijene.

6. Za polinom stepena 3

P 3 (x) = ax 3 + bx 2 + cx + d jedna od dvije stvari je moguća: ili se razlaže na proizvod tri binoma

R 3 (x) = a (h - α) (h - β) (h - γ), ili se može razgraditi na proizvod binomskog i kvadratnog trinoma R 3 (x) = a (h - α) (h 2 + βh + γ).

7. Bilo koji polinom četvrtog stepena može se razložiti na proizvod dva kvadratna trinoma.

8. Polinom f (x) je djeljiv polinomom g (x) bez ostatka ako postoji polinom q (x) takav da je f (x) = g (x) q (x). Za dijeljenje polinoma primjenjuje se pravilo “podjele ugla”.

9. Za djeljivost polinoma P (x) na binom (x - c) potrebno je i dovoljno da broj c bude korijen iz P (x) (posljedica Bezout -ove teoreme).

10. Vijetina teorema: Ako su x 1, x 2, ..., x n pravi korijeni polinoma

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, tada vrijede sljedeće jednakosti:

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0.

Primjeri rješenja

Primjer 1.

Nađi ostatak dijeljenja P (x) = x 3 + 2/3 x 2 - 1/9 sa (x - 1/3).

Rešenje.

Prema posljedici Bezout -ove teoreme: "Ostatak podjele polinoma binomom (x - c) jednak je vrijednosti polinoma u c". Pronađimo R (1/3) = 0. Dakle, ostatak je 0, a broj 1/3 je korijen polinoma.

Odgovor: R = 0.

Primjer 2.

Podijeli sa uglom 2x 3 + 3x 2 - 2x + 3 na (x + 2). Pronađi ostatak i nepotpuni količnik.

Rešenje:

2x 3 + 3x 2 - 2x + 3 | x + 2

2h 3 + 4 x 2 2x 2 - x

X 2 - 2 x

Odgovor: R = 3; privatno: 2x 2 - x.

Osnovne metode rješavanja jednadžbi viših stupnjeva

1. Uvođenje nove varijable

Metoda uvođenja nove varijable već je poznata na primjeru bikvadratnih jednadžbi. Sastoji se u činjenici da se za rješavanje jednadžbe f (x) = 0 uvodi nova varijabla (zamjena) t = xn ili t = g (x) i f (x) izražava u smislu t, dobivajući novu jednadžba r (t). Tada se rješavanjem jednadžbe r (t) nalaze korijeni:

(t 1, t 2, ..., t n). Nakon toga dobiva se niz n jednadžbi q (x) = t 1, q (x) = t 2, ..., q (x) = t n, iz kojih se nalaze korijeni izvorne jednadžbe.

Primjer 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Rešenje:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Zamjena (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 = 2, t 2 = 1. Obrnuta zamjena:

x 2 + x + 1 = 2 ili x 2 + x + 1 = 1;

x 2 + x - 1 = 0 ili x 2 + x = 0;

Odgovor: Iz prve jednadžbe: x 1, 2 = (-1 ± √5) / 2, iz druge: 0 i -1.

2. Faktorizacija grupiranjem i formulama smanjenog množenja

Temelj ovom metodom također nije novo i sastoji se u grupiranju pojmova na način da svaka grupa sadrži zajednički faktor. Da biste to učinili, ponekad morate koristiti neke umjetne metode.

Primjer 1.

x 4 - 3x 2 + 4x - 3 = 0.

Rešenje.

Zamislite - 3x 2 = -2x 2 - x 2 i grupirajte:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 = 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 = 0 ili x 2 + x - 3 = 0.

Odgovor: Nema korijena u prvoj jednadžbi, iz druge: x 1, 2 = (-1 ± √13) / 2.

3. Faktoring metodom nedefiniranih koeficijenata

Suština metode je da se izvorni polinom razlaže na faktore s nepoznatim koeficijentima. Koristeći svojstvo da su polinomi jednaki ako su im koeficijenti jednaki na istim stupnjevima, pronalaze se nepoznati koeficijenti proširenja.

Primjer 1.

x 3 + 4x 2 + 5x + 2 = 0.

Rešenje.

Polinom trećeg stepena se može proširiti na proizvod linearnog i kvadratnog faktora.

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

Rešivši sistem:

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, tj.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

Korijene jednadžbe (x + 1) (x 2 + 3x + 2) = 0 je lako pronaći.

Odgovor: -1; -2.

4. Način odabira korijena po najvećem i slobodnom koeficijentu

Metoda se temelji na primjeni teorema:

1) Bilo koji cijeli korijen polinoma sa cjelobrojnim koeficijentima je djelitelj slobodnog člana.

2) Da bi nesvodivi razlomak p / q (p je cijeli broj, q je prirodan) bio korijen jednadžbe s cjelobrojnim koeficijentima, potrebno je da broj p bude cjelobrojni djelitelj slobodnog člana a 0, i q je prirodni djelitelj vodećeg koeficijenta.

Primjer 1.

6x 3 + 7x 2 - 9x + 2 = 0.

Rešenje:

6: q = 1, 2, 3, 6.

Stoga je p/q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6.

Nakon što smo pronašli jedan korijen, na primjer - 2, nalazimo i druge korijene koristeći podjelu s kutom, metodu nedefiniranih koeficijenata ili Hornerovu shemu.

Odgovor: -2; 1/2; 1/3.

Imate li još pitanja? Niste sigurni kako riješiti jednadžbe?
Za pomoć od tutora - registrirajte se.
Prva lekcija je besplatna!

web mjesto, s potpunim ili djelomičnim kopiranjem materijala, potrebna je veza na izvor.

Na youtube kanalu naše web stranice kako biste bili u toku sa svim novim video lekcijama.

Za početak, prisjetimo se osnovnih formula stepena i njihovih svojstava.

Proizvod broja a se dogodi sam sebi n puta, možemo izraziti ovaj izraz kao a a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Snaga ili eksponencijalne jednadžbe - ovo su jednadžbe u kojima su varijable u stepenima (ili eksponentima), a baza je broj.

Primjeri eksponencijalnih jednadžbi:

V ovaj primjer broj 6 je baza, uvijek stoji pri dnu i varijabla x stepen ili indikator.

Evo još primjera eksponencijalnih jednadžbi.
2 x * 5 = 10
16 x - 4 x - 6 = 0

Pogledajmo sada kako se rješavaju eksponencijalne jednadžbe?

Uzmimo jednostavnu jednadžbu:

2 x = 2 3

Takav se primjer može riješiti čak i u umu. Vidljivo je da je x = 3. Uostalom, kako bi lijeva i desna strana bile jednake, umjesto x morate staviti broj 3.
Pogledajmo sada kako ovo rješenje treba formalizirati:

2 x = 2 3
x = 3

Da bismo riješili takvu jednadžbu, uklonili smo je identične osnove(to jest dvojke) i zapisali ono što je ostalo, to su stepeni. Dobili smo željeni odgovor.

Sada rezimirajmo našu odluku.

Algoritam za rješavanje eksponencijalne jednadžbe:
1. Potrebno je provjeriti isto da li jednadžba ima baze s desne i lijeve strane. Ako razlozi nisu isti, tražimo mogućnosti za rješavanje ovog primjera.
2. Nakon što su osnove iste, izjednačiti stupnja i riješiti rezultirajuću novu jednadžbu.

Riješimo sada nekoliko primjera:

Počnimo jednostavno.

Baze s lijeve i desne strane jednake su broju 2, što znači da možemo odbaciti bazu i izjednačiti njihove stupnjeve.

x + 2 = 4 Ovo je najjednostavnija jednadžba.
x = 4 - 2
x = 2
Odgovor: x = 2

U sljedećem primjeru možete vidjeti da su baze različite, to su 3 i 9.

3 3x - 9x + 8 = 0

Za početak prenosimo devetku na desnu stranu, dobivamo:

Sada morate napraviti iste baze. Znamo da je 9 = 3 2. Koristimo formulu stepena (a n) m = a nm.

3 3x = (3 2) x + 8

Dobivamo 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 sada možete vidjeti da su baze na lijevoj i desnoj strani iste i jednake tri, tako da ih možemo odbaciti i izjednačiti stepene.

3x = 2x + 16 dobilo je najjednostavniju jednadžbu
3x - 2x = 16
x = 16
Odgovor: x = 16.

Pogledajte sljedeći primjer:

2 2x + 4 - 10 4 x = 2 4

Prije svega, gledamo osnove, baze su različite dvije i četiri. A mi moramo biti - isti. Pretvorite četvorku formulom (a n) m = a nm.

4 x = (2 2) x = 2 2x

Koristimo i jednu formulu a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Jednačini dodajte:

2 2x 2 4 - 10 2 2x = 24

Doveli smo primjer na istu osnovu. Ali ometaju nas drugi brojevi 10 i 24. Šta s njima? Ako pažljivo pogledate, možete vidjeti da s lijeve strane ponavljamo 2 2x, evo odgovora - 2 2x možemo izvaditi iz zagrada:

2 2x (2 4 - 10) = 24

Izračunajmo izraz u zagradama:

2 4 — 10 = 16 — 10 = 6

Podijelite cijelu jednadžbu sa 6:

Zamislimo 4 = 2 2:

2 2x = 2 2 baze su iste, odbacujemo ih i izjednačujemo moći.
2x = 2 dobivamo najjednostavniju jednadžbu. Podijelimo ga sa 2 dobijemo
x = 1
Odgovor: x = 1.

Riješimo jednadžbu:

9 x - 12 * 3 x + 27 = 0

Pretvorimo se:
9 x = (3 2) x = 3 2x

Dobijamo jednačinu:
3 2x - 12 3x +27 = 0

Naše osnove su jednake 3. U ovom primjeru možete vidjeti da prve tri imaju stepen dva puta (2x) od drugog (samo x). U ovom slučaju možete riješiti metoda zamjene... Zamijenite broj s najmanjim stupnjem:

Tada je 3 2x = (3x) 2 = t 2

Zamijenite sve stepene s x u jednadžbi s t:

t 2 - 12t + 27 = 0
Dobivamo kvadratnu jednadžbu. Rešavamo preko diskriminatora, dobijamo:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Vraćanje na varijablu x.

Uzimamo t 1:
t 1 = 9 = 3 x

To je,

3 x = 9
3 x = 3 2
x 1 = 2

Pronađen je jedan korijen. Tražimo drugi, od t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Odgovor: x 1 = 2; x 2 = 1.

Na web stranici možete u odjeljku POMOĆI RJEŠITI za postavljanje pitanja od interesa, svakako ćemo vam odgovoriti.

Pridružite se grupi

Sudeći prema početku publikacije, koju ovdje izostavljamo, tekst je napisao Jurij Ignatijevič. I dobro je napisano, a problematika je aktuelna, to je jedini način da se pozove Rusija, kako to čini Mukhin ...

Bez obzira na to kako se neko odnosio prema moći naroda, Rusija je iznad nje i ne zaslužuje uvrede. Čak i od talentovanog uzbunjivača američke agencije NASA.

*

Adresa druga Mukhin Yu.I.

Dragi Jurij Ignatievich! Znam da posjećujete ove stranice. Stoga vam se obraćam direktno.

Svi cijenimo vaš nesebični rad na polju razotkrivanja laži Zapada, laži Amerike, laži pseudonaučnika i laži liberala. Sa zadovoljstvom i koristima za sebe i društvo, razmišljamo o ozbiljnim temama koje nam s vremena na vrijeme postavljate, bilo da je to meritokratija ili metafizika, ljubav prema nacionalnu istoriju ili obnavljanje pravde.

Međutim, vaše definicije naše zajedničke domovine su zbunjujuće i vrlo uznemirujuće.

Međutim, prosudite sami: kako biste okarakterizirali osobu koja je počela vrijeđati svoju majku, koja je bila bolesna i zbog toga privremeno prestala raditi?

Ali Rusija, kako god da se zove, i koliko god vlada bila dobra ili odvratna, Rusija je naša domovina. Domovina. Za nju su naši djedovi prolili krv i položili živote.

Stoga, staviti ga u rang sa snagom znači spustiti duhovno uzvišeno na nivo materijala, pa čak i niže. One. uspoređujete potpuno različite kategorije. Stvar koja je neprihvatljiva za bilo koju razumnu osobu.

Pitam vas, dragi druže. Mukhine, ozbiljno razmisli o ovome.

**

... A s jednadžbama (ovo nisam znao) situacija je sljedeća. Kako pronaći korijene kvadratna jednadžba pretpostavlja se još u starom Egiptu.

Kako pronaći korijene kubične jednadžbe i jednadžbe četvrtog stupnja pronađeno je u šesnaestom stoljeću, ali nisu mogli pronaći korijene jednadžbe petog stupnja do 2016. godine. A daleko od običnih ljudi pokušali su.

U šesnaestom stoljeću, osnivač simboličke algebre, François Viet, pokušao je pronaći korijene jednadžbe petog stupnja; u devetnaestom stoljeću, osnivač moderne više algebre, francuski matematičar Evariste Galois, pokušao je pronaći korijene jednadžbe petog stupnja; nakon njega je norveški matematičar Niels Henrik Abel pokušao pronaći korijene jednadžbi petog stupnja. odustao je i dokazao nemogućnost rješavanja jednadžbe petog stupnja u opšti pogled.

O zaslugama Abela čitamo u Wikipediji: „Abel je završio briljantnu studiju o drevnom problemu:dokazao nemogućnost da se općenito (u radikalima) riješi jednadžba 5. stupnja ...

Abel je u algebri pronašao neophodan uslov da se koren jednačine izrazi "u radikalima" u smislu koeficijenata ove jednačine. Dovoljan uvjet ubrzo je otkrio Galois, čija su se postignuća temeljila na Abelovim djelima.

Abel je naveo konkretne primjere jednadžbe petog stupnja, čiji se korijeni ne mogu izraziti u radikalima, i tako je u velikoj mjeri zatvorio drevni problem. "

Kao što vidite, ako su cijelo vrijeme pokušavali dokazati Poincaréovu teoremu i pokazalo se da je Perelman imao više sreće od ostalih matematičara, onda nakon Abela matematičari nisu uzeli jednadžbe petog stupnja.

A 2014 matematičar iz Tomska Sergej Zaikov, o kome po fotografiji možete zaključiti da je već godinama, a prema podacima iz članka o njemu, da je diplomirao na fakultetu primenjena matematika i kibernetika Tomska državni univerzitet, u toku svog rada dobio jednadžbe petog stepena. Slijepa ulica? Da, slijepa ulica! No, Sergej Zaikov se obvezao prekinuti ga.

A 2016. pronašao je načine za rješavanje jednadžbi petog stupnja u općem obliku! Učinio je ono što su matematičari Galois i Abel pokazali nemogućim.

Pokušao sam pronaći informacije o Sergeju Zaikovu na Wikipediji, ali jebi se! O matematičaru Sergeju Zaikovu i njegovom pronalaženju rešenja jednačina petog stepena nema informacija!

Činjenica da za matematičare postoji analog nobelova nagrada -Abel nagrada(Nobel je zabranio davanje nagrade matematičarima, a sada se dodjeljuje za matematički izmet, nazivajući ih "fizikom").

Ova matematička nagrada pripada u čast samog Abela koji je dokazao nemogućnost onoga što je Zaikov uradio... Međutim, samo nominacija za ovu nagradu nije dozvoljena. A Zaikov je usamljeni matematičar i ne postoje organizacije koje bi ga mogle predložiti za kandidata za ovu nagradu.

Istina, imamo Akademiju nauka, ali na kraju krajeva, akademici ne sjede tamo radi razvoja matematike, već "kako bi smanjili plijen". Kome treba ovaj Zaikov tamo?

Pa, za novinske agencije Zaikov nije Perelman za vas! Stoga, Zajkovo otkriće za medije nije senzacija.

Da je Porošenko pogriješio s vratima - da! Ovo je prava senzacija!

Tomski matematičar riješio je problem koji se nije mogao riješiti dvjesto godina

Pojavom algebre, njezin glavni zadatak smatrao se rješavanjem algebarskih jednadžbi. Rješenje jednadžbe drugog stupnja već je bilo poznato u Babilonu i Drevni Egipat... Takve jednadžbe prolazimo u školi. Sjećate li se jednadžbe x2 + ax + b = 0 i diskriminante?

Sergej Zaikov s knjigom

Rješenje algebarskih jednadžbi trećeg i četvrtog stupnja pronađeno je u šesnaestom stoljeću. Ali nije bilo moguće riješiti jednadžbu petog stupnja. Razlog je pronašao Lagrange. Pokazao je da je rješenje jednadžbi trećeg i četvrtog stupnja postalo moguće jer se mogu svesti na jednadžbe koje su već riješene. Jednačina trećeg stepena može se svesti na jednačinu drugog stepena, a jednačina četvrtog stepena na jednačinu trećeg. Ali jednadžba petog stupnja svodi se na jednadžbu šestog, odnosno složenije, stoga tradicionalne metode rješavanja nisu primjenjive.

Pitanje rješavanja jednadžbe petog stupnja pokrenulo se prije samo dvjesto godina, kada je Abel dokazao da se sve jednadžbe petog stupnja ne mogu riješiti u radikalima, odnosno u kvadratnim, kubičnim i drugim korijenima, koji su nam poznati iz škole. A Galois je uskoro, odnosno prije dvjesto godina, pronašao kriterij za određivanje koje se jednadžbe petog stupnja mogu riješiti u radikalima, a koje ne. Sastoji se u činjenici da Galoisova grupa, rješiva ​​u radikalima jednadžbe petog stupnja, mora biti ili ciklična ili metaciklična. Ali Galois nije pronašao način da u radikalima riješi one jednadžbe petog stupnja koje su rješive u radikalima. Galoisova teorija je vrlo poznata, o njoj je napisano mnogo knjiga.

Do sada su pronađena samo posebna rješenja za jednadžbe petog stupnja rješive u radikalima. I samo ove godine, Tomski matematičar Sergej Zaikov riješio je problem koji se nije mogao riješiti dvjesto godina. Objavio knjigu „Kako se rješavaju u radikalima? algebarske jednadžbe petog stepena ”, u kojem je naznačio metodu rješavanja bilo kojih jednadžbi petog stepena, koje su rješive u radikalima. Zaikov je diplomirao na Fakultetu primijenjene matematike i kibernetike na Državnom univerzitetu Tomsk. Uspeli smo da ga intervjuišemo.

- Sergej, zašto si počeo rješavati ovaj problem?

- Morao sam da rešim jednačinu petog stepena da bih rešio problem iz druge grane matematike. Počeo sam smišljati kako to pronaći i otkrio da nisu svi riješeni radikalno. Zatim sam pokušao pretražiti naučna literatura metoda za rješavanje onih jednadžbi koje su rješive u radikalima, ali su pronašle samo kriterij prema kojem se može odrediti koje su rješive, a koje ne. Nisam algebraist, ali, naravno, kao apsolvent FPMK -a, mogu primijeniti i algebarske metode. Stoga sam od 2014. godine ozbiljno počeo tražiti rješenje i sam ga pronašao.

Metod sam pronašao prije dvije godine, pripremio sam knjigu u kojoj je opisano ne samo ono, već i načini rješavanja nekih jednadžbi stepena većih od pete. Ali nisam imao novca za objavljivanje. Ove godine sam odlučio da će biti lakše objaviti samo dio ovog djela, i uzeo sam samo polovicu, posvećenu načinu rješavanja jednadžbe petog stupnja u radikalima.

Cilj mi je bio objaviti nešto poput vodiča za rješavanje ovog problema, razumljivog matematičarima koji trebaju riješiti određenu jednadžbu. Stoga sam to pojednostavio uklanjanjem mnogih dugačke formule i veliki dio teorije, smanjivši više od polovice, ostavljajući samo ono bitno. Stoga sam završio s nečim poput knjige "za lutke", prema kojoj matematičari koji nisu upoznati s Galoisovom teorijom mogu riješiti jednadžbu koja im je potrebna.

- Na tome veliko hvala Vladislavu Beresnevu, sa kojim se poznajemo dugi niz godina. Sponzorisao je objavljivanje knjige.

- Je li moguće da dobijete neku nagradu iz matematike za rješavanje ovog problema? Na primjer, spomenuli ste Abela. No, postoji li Abellova nagrada u matematici, koja se smatra analogom Nobelove nagrade?

- Ova mogućnost se ne može potpuno isključiti. Ali ni tome se ne treba nadati.

Na primjer, prijave za kandidate za nagradu Abel 2019. moraju se podnijeti do 15. septembra. Štaviše, samo-nominacija nije dozvoljena. A ja sam usamljeni matematičar. Ne postoje organizacije ili poznati matematičari koji bi me nominirali. Stoga se neće razmatrati bez obzira na to zaslužuje li moj rad ovu nagradu i je li u duhu ove nagrade dodijeljena onima koji nastavljaju Abelovo djelo. Ali čak i ako je predstavljen, sve ovisi i o nivou rada drugih kandidata.

Knjiga je namijenjena onima koji nisu upoznati s Galoisovom teorijom. Osnove Galoisove teorije date su samo u dijelu u kojem su neophodne za rješavanje jednadžbe, detaljno je opisana metoda rješenja, prikazane su tehnike koje pojednostavljuju rješenje. Veći dio knjige posvećen je primjeru rješavanja određene jednadžbe. Recenzenti knjige su doktor tehničkih nauka Gennady Petrovich Agibalov i doktor fiz. mat. Nauke, profesor Petr Andrejevič Krilov.

PREPARED ANASTASIA SKIRNEVSKAYA