Згадаймо з матеріалу попереднього уроку, прямокутний трикутником називається трикутник, якщо в нього хоча б один із кутів прямої (тобто дорівнює 90 о).

Розглянемо перша ознакарівності трикутників: якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам іншого прямокутного трикутника, то такі трикутники рівні.

Проілюструємо цей випадок:

Мал. 1. Рівні прямокутні трикутники

Доказ:

Згадаймо першу рівність довільних трикутників.

Мал. 2

Якщо дві сторони та кут між ними одного трикутника та відповідні їм дві сторони та кут між ними другого трикутника рівні, то дані трикутники рівні. Про це свідчить перша ознака рівності трикутників, тобто:

Аналогічний доказ слід і прямокутних трикутників:

.

Трикутники рівні за першою ознакою.

Розглянемо другу ознаку рівності прямокутних трикутників. Якщо катет і гострий кут одного прямокутного трикутника, що прилягає до нього, відповідно дорівнюють катету і прилеглому гострому куту іншого прямокутного трикутника, то такі трикутники рівні.

Мал. 3

Доказ:

Мал. 4

Скористаємося другою ознакою рівності трикутників:

Аналогічний доказ для прямокутних трикутників:

Трикутники рівні за другою ознакою.

Розглянемо третю ознаку рівності прямокутних трикутників: якщо гіпотенуза та прилеглий до неї кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та прилеглому куту іншого трикутника, то такі трикутники рівні.

Доказ:

Мал. 5

Згадаймо другу ознаку рівності трикутників:

Мал. 6

Дані трикутники рівні, якщо:

Оскільки відомо, що одна пара гострих кутів у прямокутних трикутників дорівнює (∠А = ∠А 1), то рівність іншої пари кутів (∠B = ∠B 1) доводиться так:

Оскільки АВ = А 1 В 1 (за умовою), ∠В = ∠В 1 , ∠А = ∠А 1 . Тому трикутники АВС і А1В1С1 рівні за другою ознакою.

Розглянемо наступну ознаку рівності трикутників:

Якщо катет і гіпотенуза одного трикутника відповідно дорівнюють катету та гіпотенузі іншого трикутника, такі прямокутні трикутники рівні.

Мал. 7

Доказ:

Сумісний накладання трикутники АВС і А 1 В 1 С 1 . Припустимо, що вершини А і А 1 і С і С 1 поєдналися накладенням, а вершина В і точка В 1 не збігаються. Саме цей випадок вказано на наступному малюнку:

Мал. 8

У цьому випадку ми можемо помітити рівнобедрений трикутникАВВ 1 (за визначенням - за умовою АВ = АВ 1). Тому за властивістю ∠АВ 1 В = ∠АВВ 1 . Розглянемо визначення зовнішнього кута. Зовнішнім кутомТрикутник називається кут, суміжний будь-якому куту трикутника. Його градусна міра дорівнює сумі двох кутів трикутника, несуміжних з ним. На малюнку вказано це співвідношення:

Мал. 9

Кут 5 є зовнішнім кутом трикутника і дорівнює ∠5 = ∠1 + ∠2. Звідси випливає, що зовнішній кут більший за кожен з кутів, несуміжних з ним.

Таким чином, ∠АВВ 1 є зовнішнім кутом для трикутника АВС та дорівнює сумі∠АВВ 1 = ∠САВ + ∠АСВ = ∠АВС = ∠САВ + 90 о. Таким чином, ∠АВ 1 В (що є гострим кутом прямокутному трикутникуАВВ 1) не може бути дорівнює куту∠АВВ 1, адже даний кут- Тупий за доведеним.

Значить, наше припущення щодо розташування точок В і В 1 виявилося неправильним, отже дані точки збігаються. Отже трикутники АВС і А 1 У 1 З 1 поєдналися накладенням. Тому вони рівні (за визначенням).

Таким чином, ці ознаки вводяться не дарма, адже їх можна використовувати при вирішенні деяких завдань.

1. Омський державний університет ().
2. Довідковий портал calc.ru().
3. Вчительський портал ().

1. № 38. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В., за редакцією Садовничого В. А. Геометрія 7. М.: Просвітництво. 2010 р.

2. Виходячи з даних, вказаних на малюнку, вкажіть рівні трикутники, якщо вони є.

3. Виходячи з даних, вказаних на малюнку, вкажіть рівні трикутники, якщо вони є. Враховуйте, що АС = AF.

4. У прямокутному трикутнику до гіпотенузи проведені медіана та висота. Кут між ними дорівнює 20 о. Визначте величину кожного з гострих кутів прямокутного трикутника.

(Ознака рівності прямокутних трикутників по катету та гіпотенузі)

Якщо катет і гіпотенуза одного прямокутного трикутника відповідно дорівнюють катету та гіпотенузі іншого прямокутного трикутника, то такі трикутники рівні.

ΔABC, ΔA 1 B 1 C 1 ,

∠C=90°, ∠C 1 =90°,

BC=B 1 C 1 , AB=A 1 B 1 ,

Довести:

ΔABC= ΔA 1 B 1 C 1

Доказ:

I. На промені BC з іншого боку точки C відкладемо відрізок CD, CD=CB.

З'єднаємо точки A та D відрізком.

На промені B 1 C 1 з іншого боку від точки C 1 відкладемо відрізок C 1 D 1 , C 1 D 1 = C 1 B 1 .

Проведемо відрізок A1D1.

ІІ. У трикутниках ACD та ACB:

З рівності трикутників випливає рівність відповідних сторін AD = AB.

Аналогічно доводиться рівність трикутників A 1 C 1 D 1 і A 1 C 1 B 1 і рівність їх сторін A 1 D 1 =A 1 B 1 .

ІІІ. Оскільки AB=A 1 B 1 , то AD=A 1 D 1 .

IV. У трикутниках ABD і A 1 B 1 D 1:

1) AB=A 1 B 1 (за умовою);

2) AD=A 1 D 1 (за доведеним);

3) BD=2BC=2B 1 C 1 =B 1 D 1 .

З рівності трикутників випливає рівність відповідних кутів: ∠B=∠B1.

Ознаки рівності прямокутних трикутників

Типи трикутників

Розглянемо три точки, що не лежать на одній прямій, і три відрізки, що з'єднують ці точки (рис. 1).

Трикутником називають частину площини, обмежену цими відрізками, відрізки називають сторонами трикутника, а кінці відрізків (три точки, що не лежать на одній прямій) – вершинами трикутника.

У таблиці 1 перелічені всі можливі типи трикутників залежно від величини їх кутів .

Таблиця 1 – Типи трикутників залежно від величини кутів

Малюнок	Тип трикутника	Визначення
	Гострокутний трикутник	Трикутник, у якого всі кути гострі , називають гострокутним
	Прямокутний трикутник	Трикутник, у якого один з кутів прямий називають прямокутним
	Тупокутний трикутник	Трикутник, у якого один з кутів тупий називають тупокутним

Гострокутний трикутник

Визначення: Трикутник, у якого всі кути гострі , називають гострокутним

Прямокутний трикутник

Визначення: Трикутник, у якого один з кутів прямий називають прямокутним

Тупокутний трикутник

Визначення: Трикутник, у якого один з кутів тупий називають тупокутним

Залежно від довжин сторін виділяють два важливі типи трикутників.

Таблиця 2 – Рівностегновий та рівносторонній трикутники

Малюнок	Тип трикутника	Визначення
	Рівностегновий трикутник	бічними сторонами, а третю сторону називають основою рівнобедреного трикутника
	Рівносторонній (правильний)трикутник	Трикутник, у якого всі три сторони рівні, називають рівностороннім чи правильним трикутником

Рівностегновий трикутник

Визначення: Трикутник, у якого дві сторони рівні, називають рівнобедреним трикутником. У цьому випадку дві рівні сторони називають бічними сторонами, а третю сторону називають основою рівнобедреного трикутника

Рівносторонній (правильний) трикутник

Визначення: Трикутник, у якого всі три сторони рівні, називають рівностороннім чи правильним трикутником

Ознаки рівності трикутників

Трикутники називають рівними, якщо їх можна поєднати накладенням .

У таблиці 3 наведено ознаки рівності трикутників.

Таблиця 3 – Ознаки рівності трикутників

Малюнок	Назва ознаки	Формулювання ознаки
	по двом сторонам та кутку між ними
	Ознака рівності трикутників по стороні та двом прилеглим до неї кутам
	Ознака рівності трикутників по трьом сторонам

Ознака рівності трикутників з обох боків і кутку між ними

Формулювання ознаки. Якщо дві сторони одного трикутника та кут між ними відповідно дорівнюють двом сторонам іншого трикутника та куту між ними, то такі трикутники рівні

Ознака рівності трикутників осторонь і двома прилеглими до неї кутами

Формулювання ознаки. Якщо сторона і два прилеглих до неї кута одного трикутника відповідно дорівнюють стороні та двох прилеглих до неї кутів іншого трикутника, то такі трикутники рівні

Ознака рівності трикутників по трьох сторонах

Формулювання ознаки. Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні

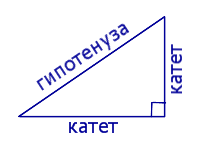
Ознаки рівності прямокутних трикутників

Для сторін прямокутних трикутників прийнято використовувати такі назви.

Гіпотенузою називають сторону прямокутного трикутника, що лежить проти прямого кута(рис. 2), дві інші сторони називають катетами.

Таблиця 4 – Ознаки рівності прямокутних трикутників

Малюнок	Назва ознаки	Формулювання ознаки
	по двом катетам	Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам іншого прямокутного трикутника, то такі прямокутні трикутники рівні
	Ознака рівності прямокутних трикутників по катету та прилеглого гострого кута	Якщо катет і гострий кут одного прямокутного трикутника, що прилягає до нього, відповідно дорівнюють катету і прилеглому до нього гострому куту іншого прямокутного трикутника, то такі прямокутні трикутники рівні
	Ознака рівності прямокутних трикутників по катету та протилежному гострому куту	Якщо катет і протилежний гострий кут одного прямокутного трикутника відповідно дорівнюють катету і протилежному гострому куту іншого прямокутного трикутника, такі прямокутні трикутники рівні
	Ознака рівності прямокутних трикутників по гіпотенузі та гострому кутку	Якщо гіпотенуза та гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі та гострому куту іншого прямокутного трикутника, то такі прямокутні трикутники рівні
	Ознака рівності прямокутних трикутників по катету та гіпотенузі	Якщо катет і гіпотенуза одного прямокутного трикутника відповідно дорівнюють катету та гіпотенузі іншого прямокутного трикутника, то такі прямокутні трикутники рівні

Ознака рівності прямокутних трикутників за двома катетами

У курсі геометрії 7 класу було вивчено, а на минулому уроці – повторено, так звані ознаки рівності трикутників. Нагадаємо їх:

1-а ознака (по 2 сторони і кут між ними):якщо у трикутників рівні дві сторони та кут між ними, то такі трикутники рівні між собою.

2-а ознака (на стороні та двох прилеглих кутах):якщо у трикутників рівні сторона і два кути, що належать до цієї сторони, такі трикутники рівні між собою. Примітка:користуючись тим, що сума кутів трикутника постійна і дорівнює, легко довести, що умова «прилежності» кутів не є необхідною, тобто ознака буде вірною і в такому формулюванні: «... рівні сторона і два кути, то …».

3-я ознака (по 3 сторонах):якщо трикутники рівні всі три сторони, то такі трикутники рівні між собою.

Звичайно, всі ці ознаки залишаються вірними і для прямокутних трикутників. Однак у прямокутних трикутників є одна істотна особливість – вони завжди мають пару рівних прямих кутів. Тому ці ознаки їм спрощуються. Отже, сформулюємо ознаки рівності прямокутних трикутників:

1-а ознака (за двома катетами):якщо у прямокутних трикутників катети попарно рівні, такі трикутники рівні між собою (див. рис. 2).

Дано:

Мал. 2. Ілюстрація першої ознаки рівності прямокутних трикутників

Довести:

Доказ:пригадаємо, що у прямокутних трикутниках: . Отже, ми можемо скористатися першою ознакою рівності трикутників (по 2 сторони та кут між ними) і отримати: .

Доведено.

2-й ознака (за катетом та кутом):якщо катет і гострий кут одного прямокутного трикутника дорівнюють катету та гострому куту іншого прямокутного трикутника, то такі трикутники рівні між собою (див. рис. 3).

Дано:

Мал. 3. Ілюстрація другої ознаки рівності прямокутних трикутників

Довести:

Доказ:Одночасно відзначимо, що те що, що рівні кути, прилеглі до рівним катетам, перестав бути важливим. Справді, сума гострих кутів прямокутного трикутника (як 1) дорівнює . Значить, якщо дорівнює одна пара з цих кутів, то дорівнює й інша (оскільки їх суми однакові).

Доказ цієї ознаки зводиться до використання другої ознаки рівності трикутників(По 2 кутах та стороні). Справді, за умовою рівні катети і пара кутів, що прилягають до них. Але друга пара прилеглих до них кутів складається з кутів. . Отже, ми можемо скористатися другою ознакою рівності трикутників і отримати: .

Доведено.

3-я ознака (з гіпотенузи та кута):якщо гіпотенуза та гострий кут одного прямокутного трикутника дорівнюють гіпотенузі та гострому куту іншого прямокутного трикутника, то такі трикутники рівні між собою (див. рис. 4).

Дано:

Мал. 4. Ілюстрація третьої ознаки рівності прямокутних трикутників

Довести:

Доказ:для доказу цієї ознаки можна одразу скористатися другою ознакою рівності трикутників– з обох боків та двох кутів (точніше, наслідком, в якому зазначено, що кути не обов'язково повинні бути прилеглими до сторони). Дійсно, за умовою: , , а з властивостей прямокутних трикутників випливає, що . Отже, ми можемо скористатися другою ознакою рівності трикутників і отримати: .

Доведено.

4-а ознака (з гіпотенузи та катету):якщо гіпотенуза і катет одного прямокутного трикутника рівні відповідно до гіпотенузи та катету іншого прямокутного трикутника, то такі трикутники рівні між собою (див. рис. 5).

Дано:

Мал. 5. Ілюстрація четвертої ознаки рівності прямокутних трикутників

Довести:

Доказ:для доказу цієї ознаки скористаємося ознакою рівності трикутників, яку ми сформулювали і довели на минулому уроці, а саме: якщо трикутники мають дві сторони і більший кут, то такі трикутники є рівними. Дійсно, за умовою у нас є дві рівних сторони. Крім того, за якістю прямокутних трикутників: . Залишилося довести, що прямий кут є найбільшим у трикутнику. Припустимо, що це не так, отже, має бути ще хоча б один кут, який більше. Але тоді сума кутів трикутника вже буде більшою. Але це неможливо, отже, такого кута в трикутнику бути не може. Значить, прямий кут є найбільшим у прямокутному трикутнику. Отже, можна скористатися сформульованою вище ознакою, і отримати: .

Доведено.

Сформулюємо тепер ще одну властивість, характерну лише для прямокутних трикутників.

Властивість

Катет, що лежить проти кута, в 2 рази менше гіпотенузи (див. рис. 6).

Дано:

Довести:AB

Доказ:виконаємо додаткову побудову: продовжимо пряму за точку на відрізок, що дорівнює . Отримаємо точку. Оскільки кути і – суміжні, їх сума дорівнює . Оскільки, то й кут.

Отже, прямокутні трикутники (за двома катетами: – загальний, – за побудовою) – перша ознака рівності прямокутних трикутників.

З рівності трикутників випливає рівність всіх відповідних елементів. Отже, . Звідки: . Крім того, (з рівності все тих самих трикутників). Отже, трикутник – рівнобедрений (оскільки в нього рівні кути на підставі), але рівнобедрений трикутник, одне із кутів якого дорівнює , – рівносторонній. З цього випливає, зокрема, що , Що й потрібно було довести.

Доведено.

4. Властивість катета, що лежить проти кута

Правильно і зворотне твердження: якщо в прямокутному трикутнику гіпотенуза вдвічі більше одного з катетів, то гострий кут, що лежить навпроти цього катета, дорівнює .

Сформулюємо ще один важливий ознака прямокутного трикутника.

Примітка:ознака означає, якщо якесь твердження правильне, то трикутник є прямокутним. Тобто ознака дозволяє ідентифікувати прямокутний трикутник.

Важливо не плутати ознаку звластивістю – тобто, якщо трикутник прямокутний, то він має такі властивості… Часто ознаки та властивості є взаємно зворотними, але не завжди. Наприклад, властивість рівностороннього трикутника: у рівносторонньому трикутнику є кут . Але це не буде ознакою рівностороннього трикутника, тому що не будь-який трикутник, який має кут є рівностороннім.

Можна навести і більше життєвий приклад: властивість слова "хліб" - у слові "хліб" 4 літери. Але наявність 4 букв не є ознакою слова «хліб», оскільки існує безліч слів із 4 букв.

5. Ознака прямокутного трикутника (медіана дорівнює половині сторони, до якої проведено)

Отже, ознака прямокутного трикутника:

Якщо у трикутнику медіана дорівнює половині сторони, до якої вона проведена, то цей трикутник є прямокутним, причому медіана проведена з вершини прямого кута.

Примітка:нагадаємо, що медіана- Лінія, що з'єднує вершину трикутника з серединою протилежної сторони (див. Рис. 7).

Дано:

Довести:

Доказ:оскільки , то трикутники – рівнобедрені. Отже, кути при основах кожного із цих трикутників рівні. Тобто, , . Тоді сума кутів трикутника дорівнює Значить . Але: , Що й потрібно було довести.

Доведено.

У цьому уроці ми розглянули основні властивості прямокутних трикутників, вивчені раніше 7 класі. Зокрема, згадали ознаки рівності, а також інші ознаки та властивості прямокутних трикутників.

Домашнє завдання

1. У прямокутному трикутнику , - бісектриса, . Знайти довжину катета, якщо див.

2. На гіпотенузі прямокутного трикутника позначили точку так, що . Доведіть, що точка рівновіддалена від точок , і .

3. Знайти гострі кути прямокутного трикутника, якщо вони відносяться як 5:13.

4. Медіана, проведена до гіпотенузи, дорівнює див.

5. У трикутнику, - бісектриса,. Відрізок на см менше відрізка. Знайти бісектрису.

Урок 5:Багатокутники

На цьому уроці ми приступимо вже до новій теміі введемо нове нам поняття «багатокутник». Ми розглянемо основні поняття, пов'язані з багатокутниками: сторони, вершини кути, опуклість та невипуклість. Потім доведемо найважливіші факти, такі як теорема про суму внутрішніх кутів багатокутника, теорема про суму зовнішніх кутів багатокутника. У підсумку ми підійдемо до вивчення окремих випадків багатокутників, які будуть розглядатися на подальших уроках.

1. Поняття «багатокутник»

В курсі геометрії ми вивчаємо властивості геометричних фігур і вже розглянули найпростіші з них: трикутники та кола. При цьому ми обговорювали і конкретні окремі випадки цих фігур, такі як прямокутні, рівнобедрені та правильні трикутники. Тепер настав час поговорити про більш загальні та складні фігури – багатокутниках.

З окремим випадком багатокутниківми вже знайомі – це трикутник (див. рис. 1).

Мал. 1. Трикутник

У самій назві вже підкреслюється, що це постать, яка має три кути. Отже, в багатокутникуїх то, можливо багато, тобто. більше, ніж три. Наприклад, зобразимо п'ятикутник (див. мал. 2), тобто. фігури з п'ятьма кутами.

Мал. 2. П'ятикутник. Випуклий багатокутник

Визначення. Багатокутник– фігура, що складається з кількох точок (більше двох) та відповідної кількості відрізків, які їх послідовно з'єднують. Ці точки називаються вершинамибагатокутника, а відрізки – сторонами. При цьому жодні дві суміжні сторони не лежать на одній прямій і жодні дві несуміжні сторони не перетинаються.

Визначення. Правильний багатокутник- Це опуклий багатокутник, у якого всі сторони та кути рівні.

Будь-який багатокутникподіляє площину на дві області: внутрішню та зовнішню. Внутрішню область також відносять до багатокутнику.

Іншими словами, наприклад, коли говорять про п'ятикутник, мають на увазі і всю його внутрішню область, і кордон. До внутрішньої області ставляться і всі точки, що лежать усередині багатокутника, тобто. точка теж відноситься до п'ятикутника (див. мал. 2).

Багатокутники ще іноді називають n-кутниками, щоб наголосити, що розглядається загальний випадок наявності якоїсь невідомої кількості кутів (n штук).

Визначення. Периметр багатокутника- Сума довжин сторін багатокутника.

Тепер треба познайомитись із видами багатокутників. Вони поділяються на опукліі невипуклі. Наприклад, багатокутник, зображений на рис. 2 є опуклим, а на Рис. 3 неопуклим.

Мал. 3. Неопуклий багатокутник

2. Випуклі та невипуклі багатокутники

Визначення 1. Багатокутникназивається опуклим, якщо при проведенні прямої через будь-яку з його сторін багатокутниклежить лише з одного боку від цієї прямої. Невипуклимиє всі інші багатокутники.

Легко уявити, що з продовження будь-якої сторони п'ятикутника на Рис. 2 він виявиться по одну сторону від цієї прямої, тобто. він опуклий. А ось при проведенні прямої через чотирикутник на Рис. 3 ми вже бачимо, що вона поділяє на дві частини, тобто. він невипуклий.

Але є й інше визначення опуклості багатокутника.

Визначення 2. Багатокутникназивається опуклим, якщо при виборі будь-яких двох внутрішніх точок і при з'єднанні їх відрізком всі точки відрізка є також внутрішніми точками багатокутника.

Демонстрацію використання цього визначення можна побачити з прикладу побудови відрізків на Рис. 2 та 3.

Визначення. Діагоналлюбагатокутника називається будь-який відрізок, що з'єднує дві не сусідні його вершини.

3. Теорема про суму внутрішніх кутів опуклого n-кутника

Для опису властивостей багатокутників існують дві найважливіші теореми про їх кутах: теорема про суму внутрішніх кутів опуклого багатокутникаі теорема про суму зовнішніх кутів опуклого багатокутника. Розглянемо їх.

Теорема. Про суму внутрішніх кутів опуклого багатокутника (n-кутника).

Де – кількість його кутів (сторон).

Доказ 1. Зобразимо на рис. 4 опуклий n-кутник.

Мал. 4. Випуклий n-кутник

З вершини проведемо усі можливі діагоналі. Вони ділять n-кутник на трикутник, т.к. кожна зі сторін багатокутника утворює трикутник, крім сторін, що належать до вершини . Легко бачити на малюнку, що сума кутів всіх цих трикутників якраз дорівнюватиме сумі внутрішніх кутів n-кутника. Оскільки сума кутів будь-якого трикутника – то сума внутрішніх кутів n-кутника:

Що й потрібно було довести.

Доказ 2. Можливий і інший доказ цієї теореми. Зобразимо аналогічний n-кутник Рис. 5 і з'єднаємо будь-яку його внутрішню точку з усіма вершинами.

.

Доведено.

З доведеної теореми випливає цікавий факт, що сума зовнішніх кутів опуклого n-кутника дорівнює від кількості його кутів (сторон). До речі, на відміну суми внутрішніх кутів.

Далі ми більш докладно працюватимемо з окремим випадком багатокутників – чотирикутниками. На наступному уроці ми познайомимося з такою фігурою, як паралелограм, та обговоримо його властивості.

Домашнє завдання

1. Чи існує опуклий багатокутник, сума кутів якого дорівнює: а); б); в)?

2. Знайдіть кути чотирикутника, якщо вони пропорційні числам 2, 3, 10 і 21. Чи опуклий чи непуклий цей чотирикутник?

3. Вершини опуклого п'ятикутника з'єднані через одну. Знайдіть суму кутів при вершинах одержаної «зірки».

Урок 6:Паралелограм

Цей урок присвячений одному з видів опуклих чотирикутників, а саме – паралелограму. Паралелограм – один із приватних видів чотирикутників, який включає такі підвиди, як прямокутник, ромб, квадрат – фігури, з якими кожен з нас знайомий ще з дитинства. Ми розглянемо визначення та властивості паралелограма, а також розв'яжемо кілька прикладів з використанням цих властивостей.

Визначення паралелограма

Минулого уроку ми розглянули поняття опуклого багатокутника. Тепер вивчимо окремий випадокбагатокутника – чотирикутник, а точніше – окремий випадок чотирикутника – паралелограм.

Паралелограм– це чотирикутник, у якого протилежні сторонипопарно паралельні (див. рис. 1).

Мал. 1. Паралелограм

Тобто, якщо дано дві паралельні прямі, які перетинають ще дві паралельні прямі, вони утворюють фігуру, що називається паралелограмом .

З того, що – паралелограм, можна зробити такі висновки: . Правильне і зворотне твердження: якщо , то чотирикутник – паралелограм.

Крім даного визначення, можна дати ще кілька еквівалентних, однак ми зупинимося саме на такому, класичному визначенніпаралелограма, і сформулюємо властивості цієї постаті, користуючись паралельністю її протилежних сторін.

Щоб встановити рівність прямокутних трикутників, достатньо знати, що два елементи одного трикутника відповідно дорівнюють двом елементам іншого трикутника (виключаючи прямий кут). Це, звичайно, не поширюється на рівність двох кутів одного трикутника двом кутам іншого трикутника.

Так як у прямокутному трикутнику кут між двома катетами прямої, а будь-які два прямі кути рівні, то з першої ознаки рівності трикутників випливає:

Якщо катети одного прямокутного трикутника відповідно дорівнюють катетам іншого, то такі трикутники рівні (рис 5).

Якщо катет і гострий кут одного прямокутного трикутника, що прилягає до нього, відповідно дорівнюють катету і прилеглому куту іншого трикутника, то такі трикутники рівні (рис. 6).

Розглянемо ще дві ознаки рівності прямокутних трикутників.

ТЕОРЕМА . Якщо гіпотенуза та гострий кут одного прямокутного трикутника дорівнюють гіпотенузі та гострому куту іншого трикутника, то такі трикутники рівні (рис. 7).

ДОВІД. З властивості 1є § випливає, що в таких трикутниках два інші гострі кути теж рівні, тому трикутники рівні за другою ознакою рівності трикутників, тобто по стороні (гіпотенузі) і двом прилеглим кутам.

Що й потрібно було довести.

ТЕОРЕМА . Якщо гіпотенуза і катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі та катету іншого трикутника, то такі трикутники рівні.

ДОВІД. Розглянемо трикутники ABC і A 1 B 1 C 1 , які мають кути C і C 1 - прямі, AB =A 1 B 1 , BC = B 1 C 1 (рис. 8).

Бо< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с острым углом B 1 A 1 C 1). Но это невозможно, поэтому вершины A и A 1 совместятся. Следовательно, полностью совместятся треугольники ABC A 1 B 1 C 1 , то есть они равны.

Що й потрібно було довести.

Теорема Піфагора

Значення її у тому, що з неї чи з її допомогою можна вивести більшість теорем геометрії. Одна з теорем дозволяє переконатися в тому, що якщо з точки поза прямою проведені до неї перпендикуляр і похилі, то: а) похилі рівні, якщо їх проекції рівні; б) та похила більша, яка має більшу проекцію.

Теорема Піфагора була першим твердженням, що зв'язало довжини сторін трикутників. Потім дізналися, як знаходити довжини сторін і кути гострокутних і тупокутних трикутників. Виникла ціла наука тригонометрія («тригон» - грецькою означає «трикутник»). Ця наука знайшла застосування у землемірі. Але ще раніше з її допомогою навчилися вимірювати уявні трикутники на небі, вершинами яких були зірки. Наразі тригонометрію застосовують навіть для вимірювання відстаней між космічними кораблями.

Користуючись властивостями площ багатокутників, ми встановимо чудове співвідношення між гіпотенузою і катетами прямокутного трикутника. Теорема, яку ми доведемо, називається теоремою Піфагора, яка є найважливішою теоремою геометрії.

Якщо дано нам трикутник,

І при тому з прямим кутом,

То квадрат гіпотенузи

Ми завжди легко знайдемо:

Катети у квадрат зводимо,

Суму ступенів знаходимо

І таким простим шляхом

До результату ми дійдемо.

ТЕОРЕМА. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

ДОВІД. Розглянемо прямокутний трикутник із катетами a, b та c (рис. 9 а).

Доведемо, що c2 = a2 + b2. Добудуємо трикутник до квадрата зі стороною a+b, оскільки показано малюнку (рис. 9 б).

Площа такого квадрата зі стороною a+b дорівнює (a+b) 2 . З іншого боку, цей квадрат складений із чотирьох рівних прямокутних трикутників, площа яких дорівнює ab, і квадрат зі стороною с, тому

Таким чином, (a + b) 2 = 2ab + c 2 звідки c 2 = a 2 + b 2 .

Що й потрібно було довести.

СЛІДСТВО 1 . У прямокутному трикутнику будь-який з катетів менше гіпотенузи.

ДОВІД. За теоремою Піфагора АВ 2 = АС 2 + ВС 2 . Оскільки ВС 2 >0, то АС 2<АВ, То есть АС<АВ.

СЛІДСТВО 2. Для будь-якого гострого кута б cosб<1.

ДОКАЗІВ. За визначенням косинуса cosб =. Але в результаті 1 було підтверджено, що АС<АВ, отже, дріб менше 1.

Прямокутні трикутники, які мають сторони виражаються цілими числами, називаються пифагоровыми трикутниками.

Можна довести, що катети a, b і гіпотенуза таких трикутників виражаються формулами a=2kmn; b=k(m 2 -n 2); c=k(m 2 +n 2), де k, m і n - натуральні числа, такі, що m>n. Трикутники, зі сторонами, довжини яких дорівнюють 3, 4, 5, називаються єгипетськими трикутниками, тому що вони були відомі ще древнім єгиптянам.

Зворотній до теореми Піфагора.

Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, то трикутник прямокутний (ознака прямокутного трикутника).

ДОВІД.

Нехай у трикутнику ABC AB 2 = AC 2 + BC 2 . Доведемо, що кут C – прямий. Розглянемо прямокутний трикутник A 1 B 1 C 1 із прямим кутом C 1 , у якого A 1 C 1 = AC та B 1 C 1 = BC. За теоремою Піфагора A 1 B 1 2 =A 1 C 1 2 +B 1 C 1 2 і, отже, A 1 B 1 2 = AC 2 +BC 2 . Але AC2 + BC2 = AB2 за умовою теореми. Отже, A 1 B 1 2 = AB 2 звідки A 1 B 1 = AB. Трикутники ABC і A 1 B 1 C 1 дорівнюють по трьох сторонах, тому< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.

Що й потрібно було довести.