Önceki dersteki materyalden, açılarından en az birinin dik açı (yani 90°'ye eşit) olması durumunda bir üçgene dik üçgen denildiğini hatırlayalım.

düşünelim ilk işaretÜçgenlerin eşitliği: Bir dik üçgenin iki bacağı sırasıyla başka bir dik üçgenin iki bacağına eşitse, bu tür üçgenler eştir.

Bu durumu örnekleyelim:

Pirinç. 1. Eşit dik üçgenler

Kanıt:

Keyfi üçgenlerin ilk eşitliğini hatırlayalım.

Pirinç. 2

Bir üçgenin iki kenarı ve aralarındaki açı ile ikinci üçgenin karşılık gelen iki kenarı ve bunlar arasındaki açı eşitse, bu üçgenler eştir. Bu, üçgenlerin eşitliğinin ilk işaretiyle gösterilir, yani:

Benzer bir kanıt dik üçgenler için de geçerlidir:

.

İlk kritere göre üçgenler eşittir.

Dik üçgenlerin eşitliğinin ikinci işaretini ele alalım. Bir dik üçgenin bacağı ve bitişik dar açısı sırasıyla başka bir dik üçgenin bacağına ve bitişik dar açısına eşitse, bu tür üçgenler eştir.

Pirinç. 3

Kanıt:

Pirinç. 4

Üçgenlerin eşitliği için ikinci kriteri kullanalım:

Dik üçgenler için benzer kanıt:

İkinci kritere göre üçgenler eşittir.

Dik üçgenlerin eşitliği için üçüncü kriteri ele alalım: Bir dik üçgenin hipotenüsü ve komşu açısı sırasıyla başka bir üçgenin hipotenüsüne ve komşu açısına eşitse, bu tür üçgenler uyumludur.

Kanıt:

Pirinç. 5

Üçgenlerin eşitliğine ilişkin ikinci kriteri hatırlayalım:

Pirinç. 6

Bu üçgenler aşağıdaki durumlarda eşittir:

Dik üçgenlerde bir çift dar açının (∠A = ∠A 1) eşit olduğu bilindiğine göre diğer açı çiftinin (∠B = ∠B 1) eşitliği şu şekilde kanıtlanır:

AB = A 1 B 1 (koşula göre) olduğundan, ∠B = ∠B 1, ∠A = ∠A 1. Bu nedenle ABC ve A 1 B 1 C 1 üçgenleri ikinci kritere göre eşittir.

Üçgenlerin eşitliği için aşağıdaki kriteri göz önünde bulundurun:

Bir üçgenin kenar ve hipotenüsü sırasıyla başka bir üçgenin kenar ve hipotenüsüne eşitse, bu tür dik üçgenler eştir.

Pirinç. 7

Kanıt:

ABC ve A 1 B 1 C 1 üçgenlerini üst üste bindirerek birleştirelim. A ve A 1 köşelerinin yanı sıra C ve C 1 köşelerinin üst üste bindirildiğini, ancak B köşe noktası ile B 1 noktasının çakışmadığını varsayalım. Bu tam olarak aşağıdaki şekilde gösterilen durumdur:

Pirinç. 8

Bu durumda fark edebiliriz ikizkenar üçgenАВВ 1 (tanım gereği - АВ = АВ 1 koşuluna göre). Dolayısıyla özelliğe göre ∠AB 1 B = ∠ABV 1 olur. Dış açının tanımına bakalım. Dış köşe Bir üçgenin herhangi bir açısına komşu olan açıdır. Derece ölçüsü, bir üçgenin kendisine komşu olmayan iki açısının toplamına eşittir. Şekil bu oranı göstermektedir:

Pirinç. 9

Açı 5, üçgenin dış açısıdır ve ∠5 = ∠1 + ∠2'ye eşittir. Buradan bir dış açının kendisine komşu olmayan açıların her birinden daha büyük olduğu sonucu çıkar.

Dolayısıyla ∠ABB 1 ABC üçgeninin dış açısıdır ve toplamına eşit∠ABV 1 = ∠CAB + ∠ACV = ∠ABC = ∠CAB + 90 o. Böylece, ∠AB 1 B (bu, dik üçgen ABC 1) olamaz açıya eşit∠АВВ 1, çünkü verilen açı- kanıtlandığı gibi aptalca.

Bu, B ve B1 noktalarının konumuna ilişkin varsayımımızın yanlış olduğu, dolayısıyla bu noktaların çakıştığı anlamına gelir. Bu, ABC ve A 1 B 1 C 1 üçgenlerinin üst üste bindiği anlamına gelir. Bu nedenle (tanım gereği) eşittirler.

Dolayısıyla bu özellikler boşuna tanıtılmamış çünkü bazı sorunları çözmek için kullanılabilirler.

1. Omsk devlet üniversitesi ().
2. Yardım portalı calc.ru ().
3. Öğretmen portalı ().

1. No. 38. Butuzov V.F., Kadomtsev S.B., Prasolov V.V., Sadovnichy V.A. Geometri 7. M.: Eğitim. 2010

2. Şekilde belirtilen verilere göre, varsa eşit üçgenleri belirtiniz.

3. Şekilde belirtilen verilere göre, varsa eşit üçgenleri işaretleyiniz. AC = AF olduğunu unutmayın.

4. Bir dik üçgende kenarortay ve yükseklik hipotenüse doğru çizilir. Aralarındaki açı 20 o'dur. Bu dik üçgenin her bir dar açısının boyutunu belirleyin.

(Bacak ve hipotenüs boyunca dik üçgenlerin eşitliğini işaretleyin)

Bir dik üçgenin kenar ve hipotenüsü sırasıyla başka bir dik üçgenin kenar ve hipotenüsüne eşitse, bu tür üçgenler eştir.

ΔABC, ΔA 1 B 1 C 1,

∠C=90°, ∠C 1 =90°,

BC=B 1 C 1 , AB=A 1 B 1 ,

Kanıtlamak:

ΔABC= ΔA 1 B 1 C 1

Kanıt:

I. C noktasının diğer tarafındaki BC ışınına CD, CD=CB parçasını çiziyoruz.

A ve D noktalarını bir doğru parçasıyla birleştirelim.

C 1 noktasının diğer tarafındaki B 1 C 1 ışınında C 1 D 1 , C 1 D 1 =C 1 B 1 parçasını çiziyoruz.

A 1 D 1 parçasını çizelim.

II. ACD ve ACB üçgenlerinde:

Üçgenlerin eşitliğinden karşılık gelen kenarların eşit olduğu sonucu çıkar: AD=AB.

Benzer şekilde A 1 C 1 D 1 ve A 1 C 1 B 1 üçgenlerinin eşitliği ve kenarlarının A 1 D 1 =A 1 B 1 eşitliği kanıtlanmıştır.

III. AB=A 1 B 1 olduğuna göre AD=A 1 D 1.

IV. ABD ve A 1 B 1 D 1 üçgenlerinde:

1) AB=A 1 B 1 (koşula göre);

2) AD=A 1 D 1 (kanıtlandığı gibi);

3) BD=2BC=2B 1 C 1 =B 1 D 1 .

Üçgenlerin eşitliğinden karşılık gelen açıların eşit olduğu sonucu çıkar: ∠B=∠B 1 .

Dik üçgenlerin eşitliğinin işaretleri

Üçgen Çeşitleri

Aynı doğru üzerinde yer almayan üç noktayı ve bu noktaları birleştiren üç doğru parçasını ele alalım (Şekil 1).

Üçgen, düzlemin bu bölümlerle sınırlanan kısmıdır, bölümlere üçgenin kenarları denir ve bölümlerin uçları (aynı düz çizgi üzerinde yer almayan üç nokta) üçgenin köşeleridir.

Tablo 1 olası tüm üçgen türlerini listelemektedir açılarının büyüklüğüne bağlı olarak .

Tablo 1 - Açıların büyüklüğüne bağlı olarak üçgen türleri

Çizim	Üçgen türü	Tanım
	Akut üçgen	olan bir üçgen tüm açılar keskindir dar açılı denir
	Sağ üçgen	olan bir üçgen açılardan biri doğru dikdörtgen denir
	Geniş üçgen	olan bir üçgen açılardan biri geniş , geniş denir

Akut üçgen

Tanım: olan bir üçgen tüm açılar keskindir dar açılı denir

Sağ üçgen

Tanım: olan bir üçgen açılardan biri doğru dikdörtgen denir

Geniş üçgen

Tanım: olan bir üçgen açılardan biri geniş , geniş denir

Kenar uzunluklarına göre İki önemli üçgen türü vardır.

Tablo 2 - İkizkenar ve eşkenar üçgenler

Çizim	Üçgen türü	Tanım
	İkizkenar üçgen	taraflar ve üçüncü tarafa ikizkenar üçgenin tabanı denir
	Eşkenar (doğru)üçgen	Üç tarafı da eşit olan üçgene eşkenar veya düzgün üçgen denir.

İkizkenar üçgen

Tanım: İki kenarı eşit olan üçgene ikizkenar üçgen denir. Bu durumda iki eşit kenar denir taraflar ve üçüncü tarafa ikizkenar üçgenin tabanı denir

Eşkenar (sağ) üçgen

Tanım: Üç tarafı da eşit olan üçgene eşkenar veya düzgün üçgen denir.

Üçgenlerin eşitliğinin işaretleri

Üçgenlere eş olmaları durumunda denir kaplama ile birleştirilebilir .

Tablo 3'te gösterilenler üçgenlerin eşitliğinin işaretleri.

Tablo 3 – Üçgenlerin eşitliğinin işaretleri

Çizim	Özellik adı	Özellik ifadesi
	İle iki kenar ve aralarındaki açı
	Üçgenlerin denkliği testi İle yan ve iki bitişik açı
	Üçgenlerin denkliği testi İle üç parti

Üçgenlerin denkliği testi iki tarafta ve aralarındaki açı

Özellik ifadesi. Bir üçgenin iki kenarı ve aralarındaki açı sırasıyla başka bir üçgenin iki kenarına ve aralarındaki açıya eşitse bu üçgenler eştir

Üçgenlerin denkliği testi bir kenar ve iki bitişik köşe boyunca

Özellik ifadesi. Bir üçgenin bir kenarı ve komşu iki açısı, başka bir üçgenin bir kenarı ve komşu iki açısına sırasıyla eşitse, bu üçgenler eştir

Üçgenlerin denkliği testi üç tarafta

Özellik ifadesi. Bir üçgenin üç kenarı sırasıyla başka bir üçgenin üç kenarına eşitse, bu üçgenler eştir

Dik üçgenlerin eşitliğinin işaretleri

Aşağıdaki isimler genellikle dik üçgenlerin kenarları için kullanılır.

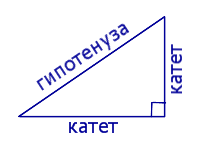
Hipotenüs dik üçgenin karşıt tarafıdır dik açı(Şekil 2), diğer iki tarafa bacak denir.

Tablo 4 – Dik üçgenlerin eşitlik işaretleri

Çizim	Özellik adı	Özellik ifadesi
	İle iki taraf	Bir dik üçgenin iki bacağı sırasıyla başka bir dik üçgenin iki bacağına eşitse, bu tür dik üçgenler eştir
	Dik üçgenler için eşitlik testi İle bacak ve bitişik dar açı	Bir dik üçgenin bacağı ve bitişik dar açısı sırasıyla başka bir dik üçgenin bacağına ve bitişik dar açısına eşitse, bu tür dik üçgenler eştir
	Dik üçgenler için eşitlik testi İle bacak ve karşı akut açı	Bir dik üçgenin bacağı ve karşı dar açısı sırasıyla başka bir dik üçgenin bacağına ve karşı dar açısına eşitse, bu tür dik üçgenler eştir
	Dik üçgenler için eşitlik testi İle hipotenüs ve dar açı	Bir dik üçgenin hipotenüsü ve dar açısı sırasıyla başka bir dik üçgenin hipotenüsüne ve dar açısına eşitse, bu tür dik üçgenler eştir
	Dik üçgenler için eşitlik testi İle bacak ve hipotenüs	Bir dik üçgenin kenar ve hipotenüsü sırasıyla başka bir dik üçgenin kenar ve hipotenüsüne eşitse, bu tür dik üçgenler eştir

İki taraftaki dik üçgenlerin eşitliğinin işareti

7.sınıf geometri dersinde son derste işleyip tekrarladığımız sözde üçgenlerin eşitliğinin işaretleri. Onlara şunu hatırlatalım:

1. işaret (2 tarafta ve aralarındaki açı):Üçgenlerin iki kenarı eşitse ve aralarındaki açı varsa bu üçgenler eştir.

2. işaret (yan ve iki bitişik açı):Üçgenlerin kenarları eşitse ve belirli bir kenara bitişik iki açı varsa, bu tür üçgenler eştir. Not: Bir üçgenin açılarının toplamının sabit ve eşit olduğu gerçeğini kullanarak, “komşu” açıların koşulunun gerekli olmadığını, yani aşağıdaki formülasyonda işaretin doğru olacağını kanıtlamak kolaydır: “. .. kenar ve iki açı eşittir, o zaman...".

3. işaret (3 tarafta):Üçgenlerin üç kenarı da eşitse bu üçgenler eştir.

Doğal olarak tüm bu işaretler dik üçgenler için de geçerlidir. Ancak dik üçgenlerin önemli bir özelliği vardır; her zaman bir çift eşit dik açıya sahiptirler. Dolayısıyla bu işaretler onlar için basitleştirilmiştir. Öyleyse dik üçgenlerin eşitlik işaretlerini formüle edelim:

1. işaret (iki tarafta): dik üçgenlerin çift olarak eşit bacakları varsa, bu tür üçgenler birbirine eşittir (bkz. Şekil 2).

Verilen:

Pirinç. 2. Dik üçgenlerin eşitliğinin ilk işaretinin çizimi

Kanıtlamak:

Kanıt: dik üçgenlerde şunu hatırlayın: . Bu, üçgenlerin eşitliğinin ilk işaretini (2 kenar ve aralarındaki açı) kullanıp şunu elde edebileceğimiz anlamına gelir: .

Kanıtlanmış.

2-th işareti (bacak ve açıya göre): bir dik üçgenin bacağı ve dar açısı başka bir dik üçgenin bacağına ve dar açısına eşitse, bu tür üçgenler birbirine eşittir (bkz. Şekil 3).

Verilen:

Pirinç. 3. Dik üçgenlerin ikinci eşitlik işaretinin çizimi

Kanıtlamak:

Kanıt: Eşit bacaklara bitişik açıların eşit olmasının esas olmadığını hemen belirtelim. Aslında, bir dik üçgenin dar açılarının toplamı (özellik 1'e göre) eşittir. Bu, eğer bu açıların bir çifti eşitse, diğerinin de eşit olduğu anlamına gelir (çünkü toplamları aynıdır).

Bu özelliğin kanıtı, kullanımıyla ilgilidir. üçgenlerin eşitliğinin ikinci işareti(2 köşede ve bir tarafta). Gerçekten de, duruma göre bacaklar ve bir çift bitişik açı eşittir. Ancak ikinci komşu açı çifti şu açılardan oluşur: . Bu, üçgenlerin eşitliği için ikinci kriteri kullanabileceğimiz ve şunu elde edebileceğimiz anlamına gelir: .

Kanıtlanmış.

3. işaret (hipotenüs ve açıya göre): bir dik üçgenin hipotenüsü ve dar açısı başka bir dik üçgenin hipotenüsüne ve dar açısına eşitse, bu tür üçgenler uyumludur (bkz. Şekil 4).

Verilen:

Pirinç. 4. Dik üçgenlerin üçüncü eşitlik işaretinin çizimi

Kanıtlamak:

Kanıt: bu işareti kanıtlamak için hemen kullanabilirsiniz üçgenlerin eşitliğinin ikinci işareti– bir tarafta ve iki açıda (daha doğrusu, açıların yana bitişik olmasının gerekmediğini belirten bir sonuç). Aslında, koşuluna göre: , , ve dik üçgenlerin özelliklerinden şu sonuç çıkar: . Bu, üçgenlerin eşitliği için ikinci kriteri kullanabileceğimiz ve şunu elde edebileceğimiz anlamına gelir: .

Kanıtlanmış.

4. işaret (hipotenüs ve kenara göre): bir dik üçgenin hipotenüsü ve kenarı sırasıyla başka bir dik üçgenin hipotenüsüne ve bacağına eşitse, bu üçgenler birbirine eşittir (bkz. Şekil 5).

Verilen:

Pirinç. 5. Dik üçgenlerin dördüncü eşitlik işaretinin çizimi

Kanıtlamak:

Kanıt: Bu kriteri kanıtlamak için, son derste formüle ettiğimiz ve kanıtladığımız üçgenlerin eşitliği kriterini kullanacağız: eğer üçgenlerin iki eşit kenarı ve daha büyük bir açısı varsa, bu tür üçgenler eşittir. Aslında, şarta göre iki tane var eşit taraflar. Ayrıca dik üçgenlerin özelliğine göre: . Geriye dik açının üçgendeki en büyük açı olduğunu kanıtlamak kalıyor. Durumun böyle olmadığını varsayalım, bu da 'den büyük en az bir açının daha olması gerektiği anlamına gelir. Ancak o zaman üçgenin açılarının toplamı zaten daha büyük olacaktır. Ancak bu imkansızdır, yani bir üçgende böyle bir açı olamaz. Bu, bir dik üçgende dik açının en büyük olduğu anlamına gelir. Bu, yukarıda formüle edilen işareti kullanabileceğiniz ve şunları elde edebileceğiniz anlamına gelir: .

Kanıtlanmış.

Şimdi yalnızca dik üçgenlerin karakteristik özelliği olan bir özelliği daha formüle edelim.

Mülk

Açının karşısındaki bacak hipotenüsten 2 kat daha küçüktür (bkz. Şekil 6).

Verilen:

Kanıtlamak:AB

Kanıt: Ek bir yapı yapalım: Düz çizgiyi noktanın ötesine eşit bir parçaya kadar uzatın. Bir noktaya değinelim. ve açıları komşu olduğundan toplamları eşittir. O zamandan beri açı.

Yani dik üçgenler (iki tarafta: - genel, - yapı itibariyle) - dik üçgenlerin eşitliğinin ilk işareti.

Üçgenlerin eşitliğinden karşılık gelen tüm elemanların eşit olduğu sonucu çıkar. Araç, . Nerede: . Ayrıca (aynı üçgenlerin eşitliğinden). Bu, üçgenin ikizkenar olduğu anlamına gelir (çünkü taban açıları eşittir), ancak açılarından biri eşit olan bir ikizkenar üçgen eşkenardır. Bundan özellikle şu sonuç çıkıyor: Kanıtlanması gereken şey buydu.

Kanıtlanmış.

4. Bir açının karşısında duran bacağın özelliği

Tersi ifadenin de doğru olduğunu belirtmekte fayda var: Bir dik üçgende hipotenüs, bacaklardan birinin iki katı büyüklüğündeyse, bu bacağın karşısındaki dar açı eşittir.

Bir başka önemli konuyu formüle edelim sağ üçgen işareti.

Not:imza herhangi bir ifade doğruysa üçgenin dik açılı olduğu anlamına gelir. Yani özellik, dik bir üçgeni tanımlamanıza olanak tanır.

Bir işareti karıştırmamak önemlidir.mülk - yani, eğer üçgen dik açılıysa, o zaman aşağıdaki özelliklere sahiptir... Çoğu zaman işaretler ve özellikler karşılıklı olarak terstir, ancak her zaman değil. Örneğin, mülkiyet eşkenar üçgen: eşkenar üçgenin bir açısı vardır . Ancak bu bir eşkenar üçgenin işareti olmayacaktır, çünkü bir açısı olan her üçgen , eşkenardır.

Daha fazlası alıntılanabilir hayat örneği: “ekmek” kelimesinin özelliği – “ekmek” kelimesinde 4 harf bulunmaktadır. Ancak 4 harfli kelimelerin sayısı çok fazla olduğundan 4 harfin varlığı “ekmek” kelimesine işaret değildir.

5. Dik üçgenin işareti (medyan çizildiği tarafın yarısına eşittir)

Bu yüzden, sağ üçgen işareti:

Bir üçgende medyan çizildiği tarafın yarısına eşitse, bu üçgen dik açılıdır ve medyan dik açının tepe noktasından çizilir.

Not:şunu hatırlatalım medyan– üçgenin tepe noktasını karşı tarafın ortasıyla birleştiren bir çizgi (bkz. Şekil 7).

Verilen:

Kanıtlamak:

Kanıt:Çünkü ise üçgenler ikizkenardır. Bu, bu üçgenlerin her birinin tabanlarındaki açıların eşit olduğu anlamına gelir. Yani , . O halde bir üçgenin açılarının toplamı So'ya eşittir. Ancak kanıtlanması gereken şey buydu.

Kanıtlanmış.

Bu dersimizde daha önce 7. sınıfta çalışılan dik üçgenlerin temel özelliklerine baktık. Özellikle eşitlik işaretlerinin yanı sıra dik üçgenlerin diğer işaretlerini ve özelliklerini hatırladılar.

Ev ödevi

1. Bir dik üçgende açıortaydır. Bacağın uzunluğunu cm ise bulunuz.

2. Bir dik üçgenin hipotenüsünde bir noktayı işaretleyin. . Noktanın ve noktalarından eşit uzaklıkta olduğunu kanıtlayın.

3. Bir dik üçgenin dar açıları 5:13 oranındaysa bulun.

4. Hipotenüse çizilen kenarortay cm'ye eşittir.

5. Bir üçgende açıortaydır. cm başına kesim segmentten daha az. Açıortayı bulun.

Ders 5:Çokgenler

Bu derste başlayacağız yeni konu ve bize yeni bir kavram kazandırıyor: “çokgen”. Çokgenlerle ilgili temel kavramlara bakacağız: kenarlar, köşe açıları, dışbükeylik ve dışbükey olmama. Daha sonra bir çokgenin iç açılarının toplamına ilişkin teorem, bir çokgenin dış açılarının toplamına ilişkin teorem gibi en önemli gerçekleri kanıtlayacağız. Sonuç olarak, ileriki derslerde ele alınacak olan çokgenlerin özel durumlarını incelemeye yaklaşacağız.

1. “Çokgen” kavramı

Geometri dersinde geometrik şekillerin özelliklerini inceliyoruz ve bunların en basitlerini zaten inceledik: üçgenler ve daireler. Aynı zamanda bu şekillerin dik, ikizkenar ve düzgün üçgen gibi özel durumlarını da tartıştık. Şimdi daha genel ve karmaşık rakamlardan bahsetmenin zamanı geldi - çokgenler.

Özel bir durumla çokgenler zaten aşinayız - bu bir üçgen (bkz. Şekil 1).

Pirinç. 1. Üçgen

İsmin kendisi zaten bunun üç açılı bir figür olduğunu vurguluyor. Bu nedenle, çokgen birçoğu olabilir, yani. üçten fazla. Örneğin bir beşgen çizelim (bkz. Şekil 2), yani. beş köşeli şekil.

Pirinç. 2. Pentagon. Dışbükey çokgen

Tanım. Çokgen- birkaç noktadan (ikiden fazla) ve bunları sırayla birbirine bağlayan karşılık gelen sayıda parçadan oluşan bir şekil. Bu noktalara denir zirvelerçokgen ve bölümler partiler. Bu durumda, iki bitişik kenar aynı düz çizgi üzerinde yer almaz ve bitişik olmayan iki kenar kesişmez.

Tanım. Düzenli çokgen tüm kenarları ve açıları eşit olan dışbükey bir çokgendir.

Herhangi çokgen Düzlemi iki alana ayırır: iç ve dış. İç alan da denir çokgen.

Yani örneğin beşgen denildiğinde hem iç bölgesinin tamamı, hem de sınırı kastediliyor. Ve iç bölge çokgenin içinde yer alan tüm noktaları içerir; bu nokta aynı zamanda beşgeni de ifade etmektedir (bkz. Şekil 2).

Çokgenlere bazen bilinmeyen sayıda açının (n adet) varlığının genel durumunun dikkate alındığını vurgulamak için n-gonlar da denir.

Tanım. Poligon çevresi– çokgenin kenarlarının uzunluklarının toplamı.

Şimdi çokgen türlerini tanımamız gerekiyor. Bunlar bölünmüştür dışbükey Ve dışbükey olmayan. Örneğin, Şekil 2'de gösterilen çokgen. 2 dışbükeydir ve Şekil 2'de. 3 dışbükey olmayan.

Pirinç. 3. Dışbükey olmayan çokgen

2. Dışbükey ve dışbükey olmayan çokgenler

Tanım 1. Çokgen isminde dışbükey, eğer kenarlarından herhangi biri boyunca düz bir çizgi çizerken, tamamı çokgen bu düz çizginin yalnızca bir tarafında yer alır. Dışbükey olmayan diğer herkes mi çokgenler.

Şekil 2'deki beşgenin herhangi bir kenarını uzatırken bunu hayal etmek kolaydır. 2 hepsi bu düz çizginin bir tarafında olacak, yani. dışbükeydir. Ancak Şekil 2'de bir dörtgen boyunca düz bir çizgi çizerken. 3'te onu iki parçaya böldüğünü zaten görüyoruz, yani. dışbükey değildir.

Ancak çokgenin dışbükeyliğinin başka bir tanımı daha var.

Tanım 2. Çokgen isminde dışbükey, eğer iç noktalarından herhangi ikisini seçip bunları bir doğru parçasına bağlarken, doğru parçasının tüm noktaları aynı zamanda çokgenin iç noktalarıysa.

Bu tanımın kullanımının bir gösterimi, Şekil 2'deki segmentlerin oluşturulması örneğinde görülebilir. 2 ve 3.

Tanım. Diyagonal Bir çokgenin bitişik olmayan iki köşesini birleştiren herhangi bir bölümdür.

3. Dışbükey bir n-gon'un iç açılarının toplamına ilişkin teorem

Çokgenlerin özelliklerini açıklamak için açılarıyla ilgili en önemli iki teorem vardır: dışbükey çokgenin iç açılarının toplamı ile ilgili teorem Ve dışbükey bir çokgenin dış açılarının toplamı ile ilgili teorem. Şimdi onlara bakalım.

Teorem. Dışbükey bir çokgenin (n-gon) iç açılarının toplamı hakkında.

Açılarının (kenarlarının) sayısı nerede?

Kanıt 1. Şekil 2'de tasvir edelim. 4 dışbükey n-gon.

Pirinç. 4. Dışbükey n-gon

Tepe noktasından mümkün olan tüm köşegenleri çiziyoruz. Bir n-gonu üçgenlere bölüyorlar çünkü çokgenin kenarlarının her biri, tepe noktasına bitişik kenarlar dışında bir üçgen oluşturur. Tüm bu üçgenlerin açılarının toplamının, n-gon'un iç açılarının toplamına tam olarak eşit olacağını şekilden görmek kolaydır. Herhangi bir üçgenin açılarının toplamı olduğuna göre, bir n-gon'un iç açılarının toplamı:

Kanıtlanması gereken şey buydu.

İspat 2. Bu teoremin başka bir ispatı da mümkündür. Şekil 2'de benzer bir n-gon çizelim. 5 ve iç noktalarından herhangi birini tüm köşelere bağlayın.

.

Kanıtlanmış.

Kanıtlanmış teoremden ilginç bir gerçek çıkar: dışbükey bir n-gon'un dış açılarının toplamı şuna eşittir: açılarının (kenarlarının) sayısına göre. Bu arada, iç açıların toplamının aksine.

Daha sonra çokgenlerin özel bir durumu olan dörtgenlerle daha ayrıntılı olarak çalışacağız. Bir sonraki derste paralelkenar gibi bir şekille tanışacağız ve özelliklerini tartışacağız.

Ev ödevi

1. Açılarının toplamı aşağıdakilere eşit olan bir dışbükey çokgen var mıdır? a) ; B) ; V)?

2. Dörtgenin açıları 2, 3, 10 ve 21 sayılarıyla orantılıysa bulun. Bu dörtgen dışbükey mi yoksa dışbükey değil mi?

3. Dışbükey bir beşgenin köşeleri birbirine bağlıdır. Ortaya çıkan “yıldızın” köşelerindeki açıların toplamını bulun.

Ders 6: Paralelkenar

Bu ders dışbükey dörtgen türlerinden birine, yani paralelkenara ayrılmıştır. Paralelkenar, her birimizin çocukluğumuzdan beri aşina olduğumuz dikdörtgen, eşkenar dörtgen, kare gibi alt türleri içeren özel dörtgen türlerinden biridir. Paralelkenarın tanımına ve özelliklerine bakacağız ve ayrıca bu özellikleri kullanarak birkaç örnek çözeceğiz.

paralelkenarın tanımı

Son dersimizde dışbükey çokgen kavramına baktık. Şimdi çalışalım özel durumçokgen - bir dörtgen veya daha doğrusu - dörtgenin özel bir durumu - paralelkenar.

Paralelkenar ile bir dörtgendir zıt taraflarçiftler halinde paralel (bkz. Şekil 1).

Pirinç. 1. Paralelkenar

Yani, iki paralel doğruyu daha kesen iki paralel doğru verilirse, bunlar paralelkenar adı verilen bir şekil oluşturur.

Paralelkenar olduğu gerçeğinden aşağıdaki sonuçlar çıkarılabilir: . Bunun tersi de doğrudur: eğer ise bu dörtgen bir paralelkenardır.

Ayrıca bu tanım, eşdeğer birkaç tane daha verebiliriz ama biz buna odaklanacağız, klasik çözünürlüklü Paralelkenar ve karşıt kenarlarının paralelliğini kullanarak bu şeklin özelliklerini formüle edin.

Dik üçgenlerin eşitliğini sağlamak için, bir üçgenin iki elemanının sırasıyla başka bir üçgenin iki elemanına (dik açı hariç) eşit olduğunu bilmek yeterlidir. Elbette bu, bir üçgenin iki açısının başka bir üçgenin iki açısına eşitliği için geçerli değildir.

Bir dik üçgende iki bacak arasındaki açı düz olduğundan ve herhangi iki dik açı eşit olduğundan, üçgenlerin eşitliğinin ilk işaretinden şu sonuç çıkar:

Bir dik üçgenin bacakları diğerinin bacaklarına karşılık gelecek şekilde eşitse, bu tür üçgenler eştir (Şekil 5).

Bir dik üçgenin bacağı ve bitişik dar açısı sırasıyla başka bir üçgenin bacağına ve bitişik açısına eşitse, bu tür üçgenler uyumludur (Şekil 6).

Dik üçgenlerin eşitliğinin iki işaretini daha ele alalım.

TEOREM . Bir dik üçgenin hipotenüsü ve dar açısı başka bir üçgenin hipotenüsüne ve dar açısına eşitse, bu üçgenler eştir (Şekil 7).

KANIT. 1є § özelliğinden, bu tür üçgenlerde diğer iki dar açının da eşit olduğu, dolayısıyla üçgenlerin ikinci eşitlik işaretine göre, yani kenar (hipotenüs) ve iki bitişik açı boyunca eşit olduğu sonucu çıkar.

Q.E.D.

TEOREM . Bir dik üçgenin hipotenüsü ve kenarı sırasıyla başka bir üçgenin hipotenüsüne ve kenarına eşitse, bu üçgenler eştir.

KANIT. ABC ve A 1 B 1 C 1 üçgenlerini düşünün, C ve C 1 açıları dik açıdır, AB = A 1 B 1 , BC = B 1 C 1 (Şekil 8).

Çünkü< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с острым углом B 1 A 1 C 1). Но это невозможно, поэтому вершины A и A 1 совместятся. Следовательно, полностью совместятся треугольники ABC A 1 B 1 C 1 , то есть они равны.

Q.E.D.

Pisagor teoremi

Önemi, geometri teoremlerinin çoğunun ondan veya onun yardımıyla çıkarılabileceği gerçeğinde yatmaktadır. Teoremlerden biri, eğer ona bir çizginin dışındaki bir noktadan dik ve eğimli bir çizgi çizilirse, o zaman: a) çıkıntıları eşitse eğimli çizgiler eşittir; b) eğimli olan daha büyüktür ve daha büyük bir çıkıntıya sahiptir.

Pisagor teoremi üçgenlerin kenarlarının uzunluklarını ilişkilendiren ilk ifadeydi. Daha sonra dar ve dik açıların kenar uzunluklarını ve açılarını bulmayı öğrendik. geniş üçgenler. Tüm trigonometri bilimi ortaya çıktı (Yunancada "trigon" "üçgen" anlamına gelir). Bu bilim arazi araştırmalarında uygulama buldu. Ancak daha önce, onun yardımıyla, köşeleri yıldız olan gökyüzündeki hayali üçgenleri ölçmeyi öğrendiler. Artık trigonometri, uzay araçları arasındaki mesafeleri ölçmek için bile kullanılıyor.

Şimdi çokgenlerin alanlarının özelliklerini kullanarak hipotenüs ile dik üçgenin kenarları arasında dikkate değer bir ilişki kuracağız. Kanıtlayacağımız teoreme geometrideki en önemli teorem olan Pisagor teoremi denir.

Eğer bize bir üçgen verilirse,

Ve buna dik bir açıyla,

Bu hipotenüsün karesi

Her zaman kolayca bulabiliriz:

Bacakları kare haline getiriyoruz,

Kuvvetlerin toplamını buluyoruz

Ve bu kadar basit bir şekilde

Sonucuna geleceğiz.

TEOREM. Bir dik üçgende hipotenüsün karesi dik kenarların karelerinin toplamına eşittir.

KANIT. Bacakları a, b ve c olan bir dik üçgeni düşünün (Şekil 9 a).

c 2 = a 2 + b 2 olduğunu kanıtlayalım. Üçgeni şekildeki gibi kenarları a+b olan bir kare şeklinde oluşturalım (Şekil 9 b).

Kenarı a + b olan böyle bir karenin alanı (a + b) 2'ye eşittir. Öte yandan, bu kare alanı ab olan dört eşit dik üçgen ve kenarı c olan bir kareden oluşuyor, yani

Böylece, (a + b) 2 =2ab + c 2, dolayısıyla c 2 = a 2 + b 2 olur.

Q.E.D.

SONUÇ 1 . Bir dik üçgende bacaklardan herhangi biri hipotenüsten küçüktür.

KANIT. Pisagor teoremine göre AB 2 = AC 2 + BC 2 . BC 2 >0 olduğuna göre AC 2<АВ, То есть АС<АВ.

SONUÇ 2. Herhangi bir dar açı b cosb için<1.

KANIT. Kosinüs cosб = tanımına göre. Ancak Sonuç 1'de AC'nin kanıtlandığı kanıtlandı.<АВ, Bu, kesrin 1'den küçük olduğu anlamına gelir.

Kenarları tamsayılarla ifade edilen dik üçgenlere Pisagor üçgenleri denir.

Bu tür üçgenlerin a, b kenarları ve hipotenüs c'nin a=2kmn; b=k(m2 -n2); c=k(m 2 +n 2), burada k, m ve n m>n olacak şekilde doğal sayılardır. Kenar uzunlukları 3, 4, 5 olan üçgenlere eski Mısırlılar tarafından bilindiği için Mısır üçgenleri adı verilmiştir.

Pisagor teoreminin tersi.

Bir üçgenin bir kenarının karesi diğer iki kenarın karelerinin toplamına eşitse, o zaman üçgen dik açılıdır (dik üçgenin işareti).

KANIT.

ABC AB 2 = AC 2 + BC 2 üçgeni olsun. C açısının dik açı olduğunu kanıtlayalım. A 1 C 1 = AC ve B 1 C 1 = BC olan, C 1 dik açılı bir A 1 B 1 C 1 dik üçgenini düşünün. Pisagor teoremine göre A 1 B 1 2 =A 1 C 1 2 +B 1 C 1 2 ve dolayısıyla A 1 B 1 2 = AC 2 +BC 2. Ancak teoremin koşullarına göre AC 2 + BC 2 = AB 2. Bu nedenle A 1 B 1 2 = AB 2, dolayısıyla A 1 B 1 = AB. ABC ve A 1 B 1 C 1 üçgenlerinin üç tarafı eşittir, dolayısıyla< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.

Q.E.D.