Genel olarak derecesi 4'ten büyük bir denklem radikallerde çözülemez. Ancak bazen, eğer onu 4'ten fazla olmayan bir dereceye kadar polinomların çarpımı olarak temsil edersek, en yüksek dereceli bir denklemde solda bulunan bir polinomun köklerini hâlâ bulabiliriz. Bu tür denklemlerin çözümü bir polinomun çarpanlara ayrılmasına dayalı olduğundan, bu makaleyi incelemeden önce bu konuyu incelemenizi öneririz.

Çoğu zaman denklemlerle uğraşmak zorundayız daha yüksek dereceler tamsayı katsayıları ile. Bu durumlarda, rasyonel kökler bulmaya çalışabilir ve ardından polinomu çarpanlara ayırabiliriz, böylece onu daha düşük dereceli, çözülmesi kolay bir denkleme dönüştürebiliriz. Bu materyalde tam da bu tür örneklere bakacağız.

Tamsayı katsayılı yüksek dereceli denklemler

a n x n + a n - 1 x n - 1 + formundaki tüm denklemler. . . + a 1 x + a 0 = 0 ise, her iki tarafı da a n n - 1 ile çarparak ve y = a n x gibi bir değişken değişikliği yaparak aynı dereceden bir denklem elde edebiliriz:

bir n x n + bir n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 an n n · x n + an n - 1 · an n n - 1 · x n - 1 + … + a 1 · (an n) n - 1 · x + a 0 · (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0

Ortaya çıkan katsayılar da tamsayı olacaktır. Bu nedenle, n'inci derecenin indirgenmiş denklemini x n + a n x n - 1 + ... + a 1 x + a 0 = 0 biçimindeki tamsayı katsayılarıyla çözmemiz gerekecek.

Denklemin tamsayı köklerini hesaplıyoruz. Denklemin tamsayı kökleri varsa, bunları serbest a 0 teriminin bölenleri arasında aramanız gerekir. Bunları bir yere yazalım ve sonucu kontrol ederek bunları birer birer orijinal eşitliğe yerleştirelim. Özdeşliği elde ettikten ve denklemin köklerinden birini bulduktan sonra bunu x - x 1 · P n - 1 (x) = 0 biçiminde yazabiliriz. Burada x 1 denklemin köküdür ve P n - 1 (x), x n + a n x n - 1 + ... + a 1 x + a 0 bölü x - x 1'in bölümüdür.

Kökler tekrarlanabileceğinden, x 1'den başlayarak P n - 1 (x) = 0 şeklinde yazılan kalan bölenleri yerine koyarız. Kimlik elde edildikten sonra kök x 2'nin bulunduğu kabul edilir ve denklem (x - x 1) (x - x 2) · P n - 2 (x) = 0 şeklinde yazılabilir. Burada P n - 2 (x), Pn - 1 (x)'in x - x 2'ye bölünmesinin bölümü olacaktır.

Bölenleri sıralamaya devam ediyoruz. Bütün kökleri bulalım ve sayılarını m olarak gösterelim. Bundan sonra orijinal denklem x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0 olarak temsil edilebilir. Burada P n - m (x), n - m dereceli bir polinomdur. Hesaplama için Horner şemasını kullanmak uygundur.

Orijinal denklemimizin tamsayı katsayıları varsa, sonuçta kesirli kökler elde edemeyiz.

Kökleri herhangi bir uygun şekilde bulunabilen P n - m (x) = 0 denklemini elde ettik. İrrasyonel veya karmaşık olabilirler.

Bu çözüm şemasının nasıl kullanıldığını özel bir örnekle gösterelim.

Örnek 1

Durum: x 4 + x 3 + 2 x 2 - x - 3 = 0 denkleminin çözümünü bulun.

Çözüm

Bütün kökleri bularak başlayalım.

Eksi üçe eşit bir serbest terimimiz var. 1, - 1, 3 ve - 3'e eşit bölenleri vardır. Bunları orijinal denklemde yerine koyalım ve hangisinin sonuçtaki özdeşlikleri verdiğini görelim.

X bire eşit olduğunda 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0 elde ederiz, bu da birin bu denklemin kökü olacağı anlamına gelir.

Şimdi x 4 + x 3 + 2 x 2 - x - 3 polinomunu (x - 1)'e bir sütunda bölelim:

Yani x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Bir özdeşliğimiz var, bu da denklemin -1'e eşit başka bir kökünü bulduğumuz anlamına geliyor.

Bir sütunda x 3 + 2 x 2 + 4 x + 3 polinomunu (x + 1)'e bölün:

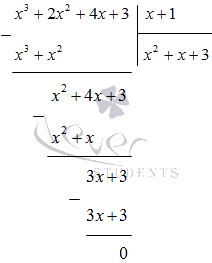
Bunu anlıyoruz

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Bir sonraki böleni - 1'den başlayarak x 2 + x + 3 = 0 eşitliğine koyarız:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Ortaya çıkan eşitlikler yanlış olacaktır, bu da denklemin artık tamsayı köklerine sahip olmadığı anlamına gelir.

Geriye kalan kökler x 2 + x + 3 ifadesinin kökleri olacaktır.

D = 1 2 - 4 1 3 = - 11< 0

Bundan şu sonuç çıkıyor ikinci dereceden üç terimli gerçek kökler yoktur ancak karmaşık eşlenik kökler vardır: x = - 1 2 ± i 11 2.

Sütunlara bölmek yerine Horner şemasının kullanılabileceğini açıklayalım. Bu şu şekilde yapılır: Denklemin ilk kökünü belirledikten sonra tabloyu doldururuz.

Katsayılar tablosunda polinomların bölünmesi bölümünün katsayılarını hemen görebiliriz; bu, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 anlamına gelir. .

Bir sonraki kök olan -1'i bulduktan sonra aşağıdakileri elde ederiz:

Cevap: x = - 1, x = 1, x = - 1 2 ± ben 11 2.

Örnek 2

Durum: x 4 - x 3 - 5 x 2 + 12 = 0 denklemini çözün.

Çözüm

Serbest terimin 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12 bölenleri vardır.

Bunları sırasıyla kontrol edelim:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Bu, x = 2'nin denklemin kökü olacağı anlamına gelir. Horner şemasını kullanarak x 4 - x 3 - 5 x 2 + 12'yi x - 2'ye bölün:

Sonuç olarak x - 2 (x 3 + x 2 - 3 x - 6) = 0 elde ederiz.

2 3 + 2 2 - 3 2 - 6 = 0

Bu, 2'nin yine kök olacağı anlamına gelir. x 3 + x 2 - 3 x - 6 = 0'ı x - 2'ye bölün:

Sonuç olarak, (x - 2) 2 · (x 2 + 3 x + 3) = 0 elde ederiz.

Kalan bölenleri kontrol etmenin bir anlamı yoktur, çünkü x 2 + 3 x + 3 = 0 eşitliği diskriminant kullanılarak çözülmesi daha hızlı ve daha uygundur.

İkinci dereceden denklemi çözelim:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Karmaşık bir eşlenik kök çifti elde ederiz: x = - 3 2 ± i 3 2 .

Cevap: x = - 3 2 ± i 3 2 .

Örnek 3

Durum: x 4 + 1 2 x 3 - 5 2 x - 3 = 0 denkleminin gerçek köklerini bulun.

Çözüm

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Denklemin her iki tarafını da 2 3 ile çarpıyoruz:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

y = 2 x değişkenlerini değiştirin:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Sonunda başardık standart denklem Standart şema kullanılarak çözülebilen 4. derece. Bölenleri kontrol edelim, bölelim ve sonuçta bunun 2 gerçek kökü y = - 2, y = 3 ve iki karmaşık kökü olduğunu anlayalım. Burada çözümün tamamını vermeyeceğiz. Yerine koyma nedeniyle bu denklemin gerçek kökleri x = y 2 = - 2 2 = - 1 ve x = y 2 = 3 2 olacaktır.

Cevap: x 1 = - 1 , x 2 = 3 2

Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.

düşünelim Bir değişkenin derecesi ikinciden yüksek olan denklemleri çözme.

P(x) = 0 denkleminin derecesi, P(x) polinomunun derecesidir, yani. sıfıra eşit olmayan katsayılı terimlerinin kuvvetlerinin en büyüğü.

Yani örneğin (x 3 – 1) 2 + x 5 = x 6 – 2 denkleminin beşinci derecesi vardır, çünkü parantezleri açıp benzerlerini getirme işlemlerinden sonra beşinci derecenin x 5 – 2x 3 + 3 = 0 eşdeğer denklemini elde ederiz.

Derecesi ikiden büyük denklemleri çözmek için ihtiyaç duyulacak kuralları hatırlayalım.

Bir polinomun kökleri ve bölenleri ile ilgili ifadeler:

1. Polinom n'inci derece n'yi aşmayan sayıda köke sahiptir ve m çokluğuna sahip kökler tam olarak m kez meydana gelir.

2. Derecesi tek olan bir polinomun en az bir gerçek kökü vardır.

3. Eğer α, P(x)'in kökü ise, o zaman P n (x) = (x – α) · Q n – 1 (x), burada Q n – 1 (x), (n – 1) dereceli bir polinomdur. .

4.

5. Tamsayı katsayılı indirgenmiş polinomun kesirli rasyonel kökleri olamaz.

6. Üçüncü dereceden bir polinom için

P 3 (x) = ax 3 + bx 2 + cx + d iki şeyden biri mümkündür: ya üç binomun çarpımına ayrıştırılır

Р 3 (x) = а(х – α)(х – β)(х – γ) veya bir binom ve bir kare trinomialin çarpımına ayrışır Р 3 (x) = а(х – α)(х 2 + βх + γ ).

7. Dördüncü dereceden herhangi bir polinom, iki kare trinomiyalin çarpımına genişletilebilir.

8. Bir f(x) polinomu, f(x) = g(x) · q(x) olacak şekilde bir q(x) polinomu varsa, kalansız bir g(x) polinomuna bölünebilir. Polinomları bölmek için “köşe bölme” kuralı kullanılır.

9. P(x) polinomunun bir binom (x – c) ile bölünebilmesi için c sayısının P(x)'in kökü olması gerekli ve yeterlidir (Bezout teoreminin sonucu).

10. Vieta teoremi: Eğer x 1, x 2, ..., x n polinomun gerçel kökleriyse

P(x) = a 0 x n + a 1 x n - 1 + ... + a n ise aşağıdaki eşitlikler sağlanır:

x 1 + x 2 + … + x n = -a 1 /a 0,

x 1 x 2 + x 1 x 3 + … + x n – 1 x n = a 2 /a 0,

x 1 x 2 x 3 + … + x n – 2 x n – 1 x n = -a 3 / a 0,

x 1 · x 2 · x 3 · x n = (-1) n an n / a 0 .

Örnekleri Çözme

Örnek 1.

P(x) = x 3 + 2/3 x 2 – 1/9 (x – 1/3) bölümünün geri kalanını bulun.

Çözüm.

Bezout teoreminin doğal sonucu olarak: "Bir polinomun binom (x – c)'ye bölümünden kalanı, c polinomunun değerine eşittir." P(1/3) = 0'ı bulalım. Dolayısıyla kalan 0 olur ve 1/3 sayısı polinomun köküdür.

Cevap: R = 0.

Örnek 2.

Bir “köşe” ile 2x 3 + 3x 2 – 2x + 3'ü (x + 2)'ye bölün. Kalanı ve eksik bölümü bulun.

Çözüm:

2x3 + 3x2 – 2x + 3| x + 2

2x 3 + 4 x 2 2x 2 – x

X 2 – 2 x

Cevap: R = 3; bölüm: 2x 2 – x.

Yüksek dereceli denklemleri çözmek için temel yöntemler

1. Yeni bir değişkenin tanıtılması

Yeni bir değişken ekleme yöntemi, iki ikinci dereceden denklem örneğinden zaten bilinmektedir. f(x) = 0 denklemini çözmek için yeni bir değişken (ikame) t = x n veya t = g(x) eklenir ve f(x) t aracılığıyla ifade edilir ve yeni bir r denklemi elde edilir. (T). Daha sonra r(t) denklemi çözülerek kökler bulunur:

(t 1, t 2, …, t n). Bundan sonra, q(x) = t 1 , q(x) = t 2 , ... , q(x) = t n şeklinde bir dizi n denklem elde edilir ve buradan orijinal denklemin kökleri bulunur.

Örnek 1.

(x 2 + x + 1) 2 – 3x 2 – 3x – 1 = 0.

Çözüm:

(x 2 + x + 1) 2 – 3(x 2 + x) – 1 = 0.

(x 2 + x + 1) 2 – 3(x 2 + x + 1) + 3 – 1 = 0.

İkame (x 2 + x + 1) = t.

t 2 – 3t + 2 = 0.

t 1 = 2, t 2 = 1. Ters ikame:

x 2 + x + 1 = 2 veya x 2 + x + 1 = 1;

x 2 + x - 1 = 0 veya x 2 + x = 0;

Cevap: İlk denklemden: x 1, 2 = (-1 ± √5)/2, ikinciden: 0 ve -1.

2. Gruplandırma ve kısaltılmış çarpma formülleriyle çarpanlara ayırma

Çözgü bu yöntem aynı zamanda yeni değildir ve terimlerin her grup ortak bir faktör içerecek şekilde gruplandırılmasından oluşur. Bunun için bazen bazı yapay tekniklerin kullanılması gerekebilir.

Örnek 1.

x 4 – 3x 2 + 4x – 3 = 0.

Çözüm.

- 3x 2 = -2x 2 – x 2'yi hayal edelim ve gruplayalım:

(x 4 – 2x 2) – (x 2 – 4x + 3) = 0.

(x 4 – 2x 2 +1 – 1) – (x 2 – 4x + 3 + 1 – 1) = 0.

(x 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.

(x 2 – 1) 2 – (x – 2) 2 = 0.

(x 2 – 1 – x + 2)(x 2 – 1 + x - 2) = 0.

(x 2 – x + 1)(x 2 + x – 3) = 0.

x 2 – x + 1 = 0 veya x 2 + x – 3 = 0.

Cevap: Birinci denklemin ikinciden kökü yoktur: x 1, 2 = (-1 ± √13)/2.

3. Belirsiz katsayılar yöntemiyle çarpanlara ayırma

Yöntemin özü, orijinal polinomun bilinmeyen katsayılarla çarpanlara ayrılmasıdır. Polinomların katsayıları aynı güçlerde eşitse eşit olması özelliğini kullanarak bilinmeyen genişleme katsayıları bulunur.

Örnek 1.

x 3 + 4x 2 + 5x + 2 = 0.

Çözüm.

3. derece bir polinom, doğrusal ve ikinci dereceden faktörlerin çarpımına genişletilebilir.

x 3 + 4x 2 + 5x + 2 = (x – a)(x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 +bx 2 + cx – ax 2 – abx – ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b – a)x 2 + (cx – ab)x – ac.

Sistemi çözdükten sonra:

(b – a = 4,
(c – ab = 5,
(-ac = 2,

(bir = -1,
(b = 3,
(c = 2, yani

x 3 + 4x 2 + 5x + 2 = (x + 1)(x 2 + 3x + 2).

(x + 1)(x 2 + 3x + 2) = 0 denkleminin köklerini bulmak kolaydır.

Cevap: -1; -2.

4. En yüksek ve serbest katsayıyı kullanarak kök seçme yöntemi

Yöntem, teoremlerin uygulanmasına dayanmaktadır:

1) Tamsayı katsayılı bir polinomun her tamsayı kökü, serbest terimin bir bölenidir.

2) İndirgenemez kesir p/q'nun (p bir tamsayı, q bir doğal sayıdır) tamsayı katsayılı bir denklemin kökü olabilmesi için, p sayısının a 0 serbest teriminin bir tamsayı böleni olması gerekir, ve q baş katsayının doğal böleni olsun.

Örnek 1.

6x3 + 7x2 – 9x + 2 = 0.

Çözüm:

6: q = 1, 2, 3, 6.

Bu nedenle p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Bir kök bulduktan sonra, örneğin – 2, köşe bölmeyi, belirsiz katsayılar yöntemini veya Horner şemasını kullanarak diğer kökleri bulacağız.

Cevap: -2; 1/2; 1/3.

Hala sorularınız mı var? Denklemleri nasıl çözeceğinizi bilmiyor musunuz?
Bir öğretmenden yardım almak için kaydolun.
İlk ders ücretsiz!

web sitesi, materyalin tamamını veya bir kısmını kopyalarken kaynağa bir bağlantı gereklidir.

Tüm yeni video derslerinden haberdar olmak için web sitemizin youtube kanalına gidin.

Öncelikle kuvvetlerin temel formüllerini ve özelliklerini hatırlayalım.

Bir sayının çarpımı A kendi kendine n defa meydana geliyorsa, bu ifadeyi a a … a=a n olarak yazabiliriz.

1. a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (bir n) m = bir nm

5. a n b n = (ab) n

7. bir n / bir m = bir n - m

Güç veya üstel denklemler – bunlar, değişkenlerin kuvvet (veya üs) cinsinden olduğu ve tabanın bir sayı olduğu denklemlerdir.

Üstel denklem örnekleri:

İÇİNDE bu örnekte 6 sayısı tabandır, her zaman alttadır ve değişken X derece veya gösterge.

Üstel denklemlere daha fazla örnek verelim.
2x*5=10
16 x - 4 x - 6=0

Şimdi üstel denklemlerin nasıl çözüldüğüne bakalım?

Basit bir denklem ele alalım:

2 x = 2 3

Bu örnek kafanızda bile çözülebilir. x=3 olduğu görülmektedir. Sonuçta sol ve sağ tarafların eşit olması için x yerine 3 sayısını koymanız gerekiyor.
Şimdi bu kararın nasıl resmileştirileceğini görelim:

2 x = 2 3
x = 3

Böyle bir denklemi çözmek için kaldırdık aynı gerekçeler(yani ikili) ve kalanları yazdık, bunlar dereceler. Aradığımız cevabı bulduk.

Şimdi kararımızı özetleyelim.

Üstel denklemi çözmek için algoritma:
1. Kontrol etmeniz gerekiyor birebir aynı Denklemin sağda ve solda tabanları olup olmadığı. Sebepler aynı değilse bu örneği çözecek seçenekler arıyoruz.
2. Tabanlar aynı hale geldikten sonra, eşitlemek derece ve ortaya çıkan yeni denklemi çözün.

Şimdi birkaç örneğe bakalım:

Basit bir şeyle başlayalım.

Sol ve sağ taraftaki tabanlar 2 sayısına eşittir, yani tabanı atıp derecelerini eşitleyebiliriz.

x+2=4 En basit denklem elde edilir.
x=4 – 2
x=2
Cevap: x=2

Aşağıdaki örnekte tabanların farklı olduğunu görebilirsiniz: 3 ve 9.

3 3x - 9x+8 = 0

İlk önce dokuzu sağ tarafa hareket ettirin, şunu elde ederiz:

Şimdi aynı temelleri yapmanız gerekiyor. 9=3 2 olduğunu biliyoruz. (a n) m = a nm güç formülünü kullanalım.

3 3x = (3 2) x+8

9 x+8 =(3 2) x+8 =3 2x+16 elde ederiz

3 3x = 3 2x+16 Artık sol ve sağ tarafta tabanların aynı ve üçe eşit olduğu açıktır, bu da onları bir kenara bırakıp dereceleri eşitleyebileceğimiz anlamına gelir.

3x=2x+16 en basit denklemi elde ederiz
3x - 2x=16
x=16
Cevap:x=16.

Aşağıdaki örneğe bakalım:

2 2x+4 - 10 4x = 2 4

Öncelikle tabanlara, ikinci ve dördüncü tabanlara bakıyoruz. Ve onların aynı olmasına ihtiyacımız var. Dördünü (a n) m = a nm formülünü kullanarak dönüştürüyoruz.

4 x = (2 2) x = 2 2x

Ayrıca a n a m = a n + m formülünü de kullanıyoruz:

2 2x+4 = 2 2x2 4

Denkleme ekleyin:

2 2x 2 4 - 10 2 2x = 24

Bunun örneğini verdik aynı gerekçelerle. Ama diğer 10 ve 24 sayıları bizi rahatsız ediyor, onlarla ne yapacağız? Yakından bakarsanız sol tarafta 2 2x'in tekrarlandığını görebilirsiniz, işte cevap: 2 2x'i parantezlerin dışına koyabiliriz:

2 2x (2 4 - 10) = 24

Parantez içindeki ifadeyi hesaplayalım:

2 4 — 10 = 16 — 10 = 6

Denklemin tamamını 6'ya bölüyoruz:

4=2 2 olduğunu varsayalım:

2 2x = 2 2 tabanlar aynı, bunları atıp dereceleri eşitliyoruz.
2x = 2 en basit denklemdir. 2'ye böleriz ve elde ederiz
x = 1
Cevap: x = 1.

Denklemi çözelim:

9 x – 12*3 x +27= 0

Hadi dönüştürelim:
9 x = (3 2) x = 3 2x

Denklemi elde ederiz:
3 2x - 12 3x +27 = 0

Tabanlarımız aynı, üçe eşit. Bu örnekte ilk üçünün derecesinin ikincinin (sadece x) iki katı (2x) olduğunu görüyorsunuz. Bu durumda çözebilirsiniz değiştirme yöntemi. Sayıyı en küçük dereceyle değiştiriyoruz:

O zaman 3 2x = (3 x) 2 = t 2

Denklemdeki tüm x kuvvetlerini t ile değiştiririz:

t2 - 12t+27 = 0
İkinci dereceden bir denklem elde ederiz. Diskriminant yoluyla çözerek şunu elde ederiz:
D=144-108=36
t1 = 9
t2 = 3

Değişkene geri dönelim X.

t 1'i alın:
t1 = 9 = 3x

Öyleyse,

3 x = 9
3 x = 3 2
x 1 = 2

Bir kök bulundu. T 2'den ikincisini arıyoruz:
t2 = 3 = 3x
3 x = 3 1
x 2 = 1
Cevap: x 1 = 2; x 2 = 1.

Web sitesinde bölümde yapabilirsiniz KARAR VERMEYE YARDIM EDİN Sorularınız varsa mutlaka cevaplayacağız.

Gruba katıl

Burada atlayacağımız yayının başlangıcına bakılırsa metin Yuri Ignatievich tarafından yazılmıştır. Ve iyi yazılmış ve konular güncel, ancak Mukhin'in yaptığı gibi Rusya'yı bu şekilde adlandırın...

Halk karşıtı güç hakkında kim ne düşünürse düşünsün, Rusya onun üstündedir ve hakareti hak etmez. Hatta Amerikan ajansı NASA'nın yetenekli yalan ifşacısından bile.

*

Yoldaş'a itiraz Muhina Yu.I.

Sevgili Yuri Ignatievich! Bu sayfaları ziyaret ettiğinizi biliyorum. Bu nedenle doğrudan size sesleniyorum.

Batı'nın yalanlarını, Amerika'nın yalanlarını, sahte bilim adamlarının yalanlarını, liberallerin yalanlarını açığa çıkarma alanındaki özverili çalışmanızı hepimiz takdir ediyoruz. Zaman zaman önümüze getirdiğiniz meritokrasi, metafizik, aşk sevgisi gibi ciddi konuları zevkle, kendimiz ve toplum için düşünüyoruz. ulusal tarih veya adaletin yeniden tesis edilmesi.

Ancak ortak Anavatanımıza ilişkin tanımlarınız kafa karıştırıcı ve çok üzücü.

Ancak siz karar verin: Hasta olan annesine hakaret etmeye başlayan ve bunun sonucunda geçici olarak çalışmayı bırakan bir kişiyi nasıl nitelendirirsiniz?

Ama Rusya, adı ne olursa olsun, hükümet ne kadar iyi ya da iğrenç olursa olsun, Rusya bizim Anavatanımızdır. Vatan. Dedelerimiz onun için kan döktüler, canlarını ortaya koydular.

Dolayısıyla onu kudretle aynı kefeye koymak, manevi yüceliği maddi, hatta aşağı seviyeye indirmek demektir. Onlar. tamamen farklı kategorileri karşılaştırıyorsunuz. Aklı başında bir insan için kabul edilemez bir şey.

Size soruyorum sevgili yoldaş. Mukhin, bunu ciddi olarak düşün.

**

...Ve denklemlerde (bunu bilmiyordum) durum şöyle. Kökler nasıl bulunur ikinci dereceden denklem Eski Mısır'da bunu tahmin etmiştim.

Kübik bir denklemin ve dördüncü dereceden bir denklemin köklerinin nasıl bulunacağı on altıncı yüzyılda keşfedildi, ancak 2016 yılına kadar beşinci dereceden bir denklemin kökleri bulunamadı. Ve bunu deneyenler sadece sıradan insanlar değildi.

On altıncı yüzyılda sembolik cebirin kurucusu Francois Viète, beşinci dereceden denklemlerin köklerini bulmaya çalıştı; on dokuzuncu yüzyılda modern yüksek cebirin kurucusu Fransız matematikçi Evariste Galois, denklemlerin köklerini bulmaya çalıştı. beşinci dereceden denklemler; ondan sonra Norveçli matematikçi Niels Henrik Abel, beşinci dereceden denklemlerin köklerini bulmaya çalıştı ve sonunda pes etti ve beşinci dereceden bir denklemi çözmenin imkansızlığını kanıtladı. genel görünüm.

Vikipedi'de Abel'ın erdemleri hakkında şunları okuyoruz: "Abel eski bir soruna ilişkin mükemmel bir çalışmayı tamamladı:5. dereceden bir denklemi genel biçimde (köklerde) çözmenin imkansızlığını kanıtladı ...

Cebirde Abel bulundu gerekli koşul denklemin kökünün bu denklemin katsayıları aracılığıyla “köklerle” ifade edilebilmesi için. Yeterli koşul, başarıları Abel'ın çalışmalarına dayanan Galois tarafından kısa sürede keşfedildi.

Abel, kökleri radikallerle ifade edilemeyen 5. dereceden denklemlerin somut örneklerini vererek kadim problemi büyük ölçüde kapattı.”

Gördüğünüz gibi, eğer Poincaré teoremini her zaman kanıtlamaya çalıştılarsa ve Perelman diğer matematikçilerden daha başarılı çıktıysa, Abel'den sonra matematikçiler beşinci dereceden denklemleri ele almadılar.

Ve 2014'te Tomsk'lu matematikçi Sergei Zaikov Hakkında zaten yıllar olduğu fotoğraftan ve fakülte mezunu olduğu hakkındaki makaledeki bilgilerden anlaşılabilecek kişi uygulamalı matematik ve sibernetik Tomsky devlet üniversitesiÇalışması sırasında beşinci dereceden denklemler elde etti. Çıkmaz sokak mı? Evet, bu bir çıkmaz sokak! Ancak Sergei Zaikov bunu kırmayı üstlendi.

Ve 2016'da beşinci derece denklemleri genel biçimde çözmenin yollarını buldu! Matematikçiler Galois ve Abel'in imkansız olduğunu kanıtladığı şeyi yaptı.

Wikipedia'da Sergei Zaikov hakkında bilgi bulmaya çalıştım ama canın cehenneme! Matematikçi Sergei Zaikov ve beşinci dereceden denklemlere nasıl çözüm bulduğu hakkında bilgi yok!

Meseleye keskinlik katan şey, matematikçiler için bir analogun var olmasıdır. Nobel Ödülü -Habil Ödülü(Nobel matematikçilere ödül verilmesini yasakladı ve şimdi onlar onları “fizik” olarak adlandırarak matematiksel dışkı olarak veriyorlar).

Bu matematik ödülü aynı Abel'ın onuruna verilmiştir. Zaikov'un yaptığının imkansızlığını kanıtladı. Ancak bu ödüle kendi kendine aday gösterilmek yasaktır. Ancak Zaikov yalnız bir matematikçi ve onu bu ödüle aday gösterebilecek hiçbir kuruluş yok.

Doğru, Bilimler Akademisi var ama akademisyenler orada matematiği geliştirmek için değil, “para kazanmak” için oturuyorlar. Orada bu Zaikov'a kimin ihtiyacı var?

Haber ajansları için Zaikov Perelman değil! Bu nedenle Zaikov'un medya açısından keşfi bir sansasyon değil.

Evet Poroşenko yanlış kapıyı çaldı! Bu gerçek bir sansasyon!

Tomsk'lu matematikçi iki yüz yıldır çözülemeyen bir problemi çözdü

Cebirin ortaya çıkışıyla birlikte asıl görevinin cebirsel denklemlerin çözümü olduğu düşünülmeye başlandı. İkinci dereceden bir denklemin çözümü Babil'de biliniyordu. Eski Mısır. Okulda buna benzer denklemlerden geçiyoruz. x2 + ax + b = 0 denklemini ve diskriminantı hatırlıyor musunuz?

Sergey Zaikov bir kitapla

Üçüncü ve dördüncü dereceden cebirsel denklemlerin çözümü on altıncı yüzyılda bulundu. Ancak beşinci derece denklemi çözmek mümkün olmadı. Lagrange bunun nedenini buldu. Üçüncü ve dördüncü dereceden denklemlerin çözümünün, daha önce çözülmüş denklemlere indirgenebilmesi nedeniyle mümkün olduğunu gösterdi. Üçüncü dereceden bir denklem ikinci dereceden bir denkleme, dördüncü dereceden bir denklem de üçüncü dereceden bir denkleme indirgenebilir. Ancak beşinci dereceden bir denklem altıncı dereceden bir denkleme indirgenir, yani daha karmaşıktır, dolayısıyla geleneksel yöntemlerçözümler geçerli değildir.

Beşinci dereceden bir denklemi çözme sorunu yalnızca iki yüz yıl önce, Abel beşinci dereceden tüm denklemlerin radikallerde, yani kare, küp ve okuldan bildiğimiz diğer köklerde çözülemeyeceğini kanıtladığında ilerledi. . Ve Galois çok geçmeden, yani iki yüz yıl önce, beşinci dereceden hangi denklemlerin radikallerde çözülebileceğini ve hangilerinin çözülemeyeceğini belirlemeye izin veren bir kriter buldu. Beşinci dereceden bir denklemin radikallerinde çözülebilen Galois grubunun döngüsel veya metasiklik olması gerektiği gerçeğinde yatmaktadır. Ancak Galois, radikallerde çözülebilen beşinci dereceden denklemleri radikallerde çözmenin bir yolunu bulamadı. Galois teorisi çok meşhurdur, hakkında pek çok kitap yazılmıştır.

Şimdiye kadar radikallerle çözülebilen beşinci dereceden denklemler için yalnızca kısmi çözümler bulunmuştu. Ve ancak bu yıl Tomsk matematikçisi Sergei Zaikov, iki yüz yıldır çözülemeyen bir sorunu çözdü. “Radikaller nasıl karar verir” kitabını yayınladı cebirsel denklemler Beşinci derece”, burada radikallerde çözülebilen beşinci dereceden herhangi bir denklem için bir çözüm yöntemi gösterdi. Zaikov, Tomsk Devlet Üniversitesi Uygulamalı Matematik ve Sibernetik Fakültesi mezunudur. Kendisiyle röportaj yapmayı başardık.

— Sergey, neden bu sorunu çözmeye başladın?

— Matematiğin başka bir dalındaki bir problemi çözmek için beşinci dereceden bir denklemin çözümüne ihtiyacım vardı. Onu nasıl bulacağımı bulmaya başladım ve hepsinin radikallerde çözülmediğini öğrendim. Sonra bulmaya çalıştım bilimsel literatür Radikallerde çözülebilen denklemleri çözmenin bir yolu, ancak yalnızca hangilerinin çözülebilir hangilerinin çözülemeyeceğini belirleyebilecek bir kriter bulundu. Ben bir cebirci değilim ama elbette FPMK mezunu olarak başvurabilirim ve cebirsel yöntemler. Bu nedenle 2014 yılında ciddi bir şekilde çözüm aramaya başladım ve kendim buldum.

Yöntemi iki yıl önce buldum, sadece bunun anlatıldığı değil, aynı zamanda beşten büyük bazı kuvvet denklemlerinin çözüm yöntemlerinin de anlatıldığı bir kitap hazırladım. Ama yayınlayacak param yoktu. Bu yıl bu çalışmanın yalnızca bir kısmını yayınlamanın daha kolay olacağına karar verdim ve radikallerde beşinci derece denklemin çözümüne yönelik bir yönteme ayrılan yalnızca yarısını aldım.

Amacım, bu problemi çözmeye yönelik, belirli bir denklemi çözmesi gereken matematikçiler için anlaşılır bir kılavuz gibi bir şey yayınlamak. Bu nedenle birçok şeyi kaldırarak basitleştirdim uzun formüller ve teorinin önemli bir kısmı yarıdan fazla kesilerek yalnızca gerekli olanı bırakıldı. Bu nedenle Galois teorisine aşina olmayan matematikçilerin ihtiyaç duydukları denklemi çözebilecekleri "aptallar için" kitap gibi bir şey buldum.

— Bunun için uzun yıllardır tanıdığımız Vladislav Beresnev'e çok teşekkür ederiz. Kitabın basımına sponsor oldu.

— Bu problemi çözdüğünüz için matematikte herhangi bir ödül almanız mümkün mü? Mesela Abel'dan bahsettin. Peki matematikte Nobel Ödülü'ne benzer sayılan bir Abel Ödülü var mı?

"Bu olasılık tamamen göz ardı edilemez." Ama bunu da ummamalısın.

Örneğin, 2019 Abel Ödülü adaylarının başvuruları 15 Eylül'e kadar yapılacak. Üstelik kendi kendini aday göstermeye izin verilmiyor. Ve ben yalnız bir matematikçiyim. herhangi bir kuruluş veya kuruluş bulunmamaktadır. ünlü matematikçiler adaylığımı kim önerecek? Bu nedenle çalışmamın bu ödülü hak edip etmediğine ve Abel'in çalışmalarını sürdürenlere bu ödülün verilmesinin bu ödülün ruhuna uygun olup olmadığına bakılmaksızın değerlendirmeye alınmayacaktır. Ancak sunulsa bile her şey diğer adayların çalışma düzeyine de bağlıdır.

Kitap Galois teorisine aşina olmayanlar için hazırlanmıştır. Galois teorisinin temelleri sadece denklemin çözümü için gerekli olduğu kısımda verilmekte, çözüm yöntemi ayrıntılı olarak anlatılmakta ve çözümü basitleştiren teknikler gösterilmektedir. Kitabın önemli bir kısmı belirli bir denklemi çözme örneğine ayrılmıştır. Kitabın eleştirmenleri Teknik Bilimler Doktoru Gennady Petrovich Agibalov ve Fizik Doktoru'dur. mat. Bilimler, Profesör Petr Andreevich Krylov.

TEDARİKLİ ANASTASIA SKIRNEVSKAYA